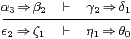
|



This section and the next summarise the symbolic language for ASD in a “user manual” style. Beware, however, that the manual for some device does not make its engineering redundant, and indeed the development of the more powerful devices of the future depends on advances in the underlying principles. Nevertheless, the constructions in the rest of this paper will be made entirely within this calculus. We repeat that there is no underlying set theory, and that the monadic and Phoa principles are unalienable parts of the system. On the other hand, there are other formulations of Scott continuity of various strengths besides the one that we give here.
Axiom 4.1 The types of ASD are generated from
We do not introduce general exponentials YX, infinitary products, type variables or dependent types — at least, not in this version of the calculus. We will explain Σ-split subspaces, which abstract Proposition 2.15, in the next section; they will be used to define open, closed and retract subspaces, and, of course, R itself.
Axiom 4.2
The logical terms of type Σ or ΣU
(also known as propositions and predicates respectively)
are generated from
These terms are generated within a larger calculus that also includes
Discrete, Hausdorff, overt and compact spaces will be defined shortly. Existential quantification over ℕ or ℝ is allowed, but universal quantification is not. Universal quantification over the closed interval I≡[0,1] is justified in Section 10.
So examples of invalid logical formulae include
| λ n.n+3, λ x. | ∛ |
| , π=ℝ3.14159, ∀ n.∃ p q.2 n=p+q and ∀ x.x2≠ −1, |
but (∃ n p q r:ℕ.pn+qn=rn) and (∀ x:|x|≤ 2.x2< 0) are fine. Programs to which an Ml compiler would assign the types nat→nat or real→real are treated in ASD as terms of type ℕ→ℕ⊥ or ℝ→ℝ⊥ [D][F].
Binding, renaming, duplication, omission and substitution for variables are the same as in the λ- and predicate calculi. A quantified formula has the same type as its body (φ), whilst λ-abstraction and application modify types in the usual way. Alternating quantifiers are allowed to any depth — so long as their ranges are overt or compact spaces.
Axiom 4.3 The numerical terms of type ℕ are generated from
Definition 4.4 Judgements in the calculus are
of the four forms
| ⊢ X type, Γ ⊢ a:X, Γ ⊢ a=b:X and Γ ⊢ α⊑β:ΣX, |
asserting well-formedness of types and typed terms, and equality or implication of terms. We shall refer to a=b and α⊑β on the right of the ⊢ as statements. On the left is the context Γ, consisting of assignments of types to variables, and maybe also equational hypotheses (Section E 2).
The form Γ ⊢ α⊑β:ΣX is syntactic sugar:
Axiom 4.5
The predicates and terms satisfy certain equational axioms,
including
| φ ⊑ ψ to mean φ∧ψ = φ, or equivalently φ∨ψ = ψ, |
Remark 4.6 Predicates and terms on their own
denote open subspaces and continuous functions respectively,
but their expressive power is very weak.
We introduce implications into the logic, but make their
hierarchy explicit, in the form of statements and judgements.
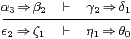
|
Our convention is that λ-application binds most tightly, followed by the propositional relations, then ∧, then ∨, then λ, ∃ and ∀, then ⇒, ⇔, ⊑, = and finally ⊢. This reflects the hierarchy of propositions, predicates, statements, judgements and rules. We often bracket propositional equality for emphasis and clarity.
Axiom 4.7 In addition to the equations for a
distributive lattice, Σ satisfies the rules1
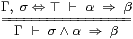
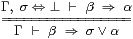
|
Axiom 4.8 Every F:ΣΣ is monotone,
i.e. F⊥⇒ F⊤.
Lemma 4.9 Σ satisfies the Phoa principle,
Fσ ⇔ F⊥ ∨ σ∧ F⊤,
for F:Σ→Σ and σ:Σ,
possibly involving parameters. ▫
Plainly Phoa entails monotonicity, and we shall explain shortly why the Gentzen-style rules in Axiom 4.7 are also derivable from it.
Definition 4.10
We say that φ:ΣX classifies an open
subspace of X, and co-classifies a closed one.
In symbols, for a:X,
| a∈ U (open) if φ a⇔ ⊤ and a∈ C (closed) if φ a⇔ ⊥, |
so U⊂ U′ iff C′⊂ C iff φ⊑φ′. This means that
| open subspaces of X, closed subspaces of X and continuous functions X→Σ |
are in bijection. A clopen, complemented or decidable subspace is one that is both open and closed. Then it and its complement are the inverse images of 0,1∈2 under some (unique) map X→2 Theorem B 11.8 [Proposition C 9.6].
Remark 4.11
Such inverse image types cannot of course be generated from
ℕ and Σ by × and Σ(−).
Our comments here will be justified by the introduction of open and
closed subspaces as Σ-split subspaces in the next section.
Briefly, being Σ-split means that all open subsubspaces of
a subspace are restrictions of open subspaces of the ambient space,
indeed in a canonical way.
Consider the left-hand Gentzen rule in terms of the open subspaces that α, β and σ classify. The top line expresses the containment α⇒β of open subsubspaces of the open subspace classified by σ. In the ambient space, this means that α∧σ⇒β∧σ, or, more briefly, α∧σ⇒β, as in the bottom line.
The rule on the right says exactly the same thing, but for the intersection of closed subspaces. Translating this into a result about relatively open subsubspaces of the closed subspace, the relative containment β⇒α in the closed subspace means β∨σ⇒α∨σ, or just β⇒α∨σ, in the whole space.
Another “extensional” aspect of topology that the rules state is that, if the inverse images of ⊤ under φ,ψ:X⇉Σ coincide as (open) subspaces of X, then x:X⊢φ x⇔ψ x (or φ=ψ) as logical terms. The inverse images of ⊥ behave in a similar way [Section C 5].
Subspaces of X2 or X3 are often called binary or ternary relations. In particular, open binary relations are the same thing as predicates with two variables.
Definition 4.12
If the diagonal subspace, X⊂ X× X, is open or closed
then we call X discrete or Hausdorff respectively.
Type-theoretically, such spaces are those in which
we may internalise equality-statements as predicates:
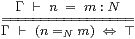
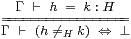
|
Lemma 4.13 Equality has the usual properties of substitution, reflexivity,
symmetry and transitivity,
whilst inequality or apartness obeys their lattice duals:
|
(The proof of this uses Axiom 4.7.) In an overt discrete space, or a compact Hausdorff one, we have the converse of the first of the four rules:
| ∃ m.φ m∧(n=m) ⇔ φ n ∀ h.φ h∨(h≠ k) ⇔ φ k. |
When both =X and ≠X are defined, as they are for ℕ, they are complementary:
| (n=X m)∨(n≠X m) ⇔ ⊤ and (n=X m)∧(n≠X m) ⇔ ⊥. |
In this case X is said to have decidable equality. ▫
Definition 4.14
A space X that admits existential or universal quantification is
called overt or compact respectively.
By these quantifiers we mean the type-theoretic rules
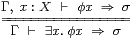
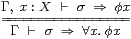
|
Axiom 4.15 The space ℕ is overt.
This and Scott continuity break the de Morgan-style lattice duality
that the other rules enjoy.
Remark 4.16
So long as the types of the variables really are overt or compact,
we may reason with the quantifiers in the usual ways:
However, we must observe the caveats in Remarks 3.5 and 15.4:
Exercise 4.17
Use the Phoa principle to prove the Frobenius and modal laws
|
where the type of x is both overt and compact. The Frobenius law for ∀ is another feature that ASD has in common with classical but not intuitionistic logic; it was nevertheless identified in intuitionistic locale theory by Japie Vermeulen [Ver94]. ▫
Lemma 4.18 Any topology ΣX has joins indexed by overt objects
and meets indexed by compact ones:
| ⋁N≡∃NX :(ΣX)N≅(ΣN)X—→ΣX and ⋀K≡∀KX :(ΣX)K≅(ΣK)X—→ΣX. |
Binary meets distribute over joins by the Frobenius law, and “substitution under the quantifier” means that all inverse image maps Σf:ΣY→ΣX , where
| Σfψ ≡ ψ· f ≡ λ x.ψ(f x) or Σf V ≡ f*V ≡ f−1V ≡ {x ∣ ψ x}, |
preserve all joins indexed by overt objects, and meets indexed by compact ones [Section C 7]. ▫
Since ℕ is overt but not compact, each ΣX has and each Σf preserves ℕ-indexed joins, but not ℕ-indexed meets.
Remark 4.19 We often want the quantifiers or meets and joins to range over
dependent types, even though we have not provided these in the calculus.
The most pressing case of this is the join or existential quantifier indexed by an open subspace M⊂ N of an overt space. This subspace is classified by a predicate α:ΣN, which we shall write as Γ, n:N ⊢ αn:Σ. The M-indexed family φm:ΣX of which we want to form the join may always be considered to be the restriction to M of an N-indexed family, so we have
| ⋁m:Mφm ≡ ∃ n:N.αn∧φn:ΣX. |
This sub- and super-script notation, which is used extensively in [G], indicates co- and contra-variance with respect to an imposed order relation, such as the arithmetical order in ℚ or inclusion of lists.
We shall also want to define both quantifiers over the closed interval [d,u], where d and u need not be constants, but we shall cross this bridge when we come to it, in Section 10.
Definition 4.20 Such a pair of families (αn,φn)
is called a directed diagram, and the corresponding
| ⋁n:αn↑φn ≡ ∃ n.αn∧φn |
is called a directed join, if (a) (∃ n.αn)⇔⊤, and (b) αn @ m⇔αn∧αm and φn @ m⊒φn∨φm for some binary operation @:N× N→ N.
In this, αn∧αm means that both φn and φm contribute to the join, so for directedness in the informal sense, we require some φn @ m to be above them both (contravariance), and also to count towards the join, for which αn @ m must be true (covariance). Hence the imposed order relation on N is that for which (N,@) is essentially a meet semilattice.
This allows us to formalise Scott continuity (Definitions 2.6 and 3.1).
Axiom 4.21 Any F:ΣΣX (possibly with parameters)
preserves directed joins in the sense that
| F(∃ n.αn∧φn) ⇔ ∃ n.αn∧ Fφn. |
Notice that F is attached to φn and not to αn, since the join being considered is really that over the subset M≡{n ∣ αn}⊂ N. The principal use of this axiom in this paper is Proposition 7.12, where the ambient overt object N is ℚ, and its imposed order is either the arithmetic one or its reverse, so @ is either max or min. Scott continuity is also what connects our definition of compactness with the traditional “finite open sub-cover” one (Remark 10.10), whilst in denotational semantics it gives a meaning to recursive programs.
In locale theory [Joh82], the homomorphisms are those of finite meets and arbitrary joins. Since we have just taken care of (some of) the directed joins, in ASD we need only consider the finitary connectives ⊤, ⊥, ∧ and ∨.
Definition 4.22
A term P of type ΣΣX is called prime
if it preserves all four lattice connectives:
| P⊤⇔⊤ P⊥⇔⊥ P(φ∧ψ)⇔ Pφ∧ Pψ P(φ∨ψ)⇔ Pφ∨ Pψ. |
The type X is said to be sober if every prime P corresponds to a unique term a:X (which we call focusP) such that
| φ(focusP)⇔ Pφ or P = λφ.φ a. |
Proposition 4.23
Let i:X→ Y between sober objects.
If the map Σi:ΣY→ΣX has an inverse I,
then so does i itself [Tay91].
Proof The map η:Y↣ΣΣY given by y↦λψ.ψ y is mono, because focusY(λψ.ψ y)=y.
Since I is an isomorphism, both it and P≡λφ.Iφ y preserve all four lattice operations, i.e. P is prime. Then, as X is sober, we may define j:Y→ X by j y≡focusX(λφ.Iφ y). It satisfies
| j(i x) = focusX(λφ.Iφ(i x)) = focusX(λφ.I(Σiφ)x) = focusX(λφ.φ x) = x |
| and λψ.ψ(i(j y)) = λψ.(Σiψ)(focusX(λφ.Iφ y)) = λψ.I(Σiψ)y = λψ.ψ y ≡ ηY y, |
so i(j y)=y since η:Y↣ΣΣY is mono. ▫
For ℕ, sobriety is equivalent to a more familiar idiom of reasoning that characterises singleton predicates, φ={n}≡(λ m.n=m). This is only meaningful for (overt) discrete objects, but we shall see in Section 14 that Dedekind completeness expresses sobriety of ℝ.
Axiom 4.24
A predicate φ n for n:ℕ (possibly involving other parameters)
is called a description if it is “uniquely satisfiable”
in the sense that
| (∃ n.φ n) ⇔ ⊤ and (φ n∧φ m) =⇒ (n =ℕm) |
are provable. Then we may introduce the n.φ n:ℕ, with the same parameters, satisfying
| φ m ⇔ (m=ℕthe n.φ n). |
Descriptions may be used to define general recursion (minimalisation) [A][D][O].
Proposition 4.25 All types that are definable from 1,
Σ and ℕ using × and Σ(−) are sober.
Proof
| focusX× Y P = <focusX(λφ.P(λ p.φ(π0 p))), focusY(λψ.P(λ p.ψ(π1 p)))>. |
Examples 4.26 We conclude with some examples of the four main topological
properties.
| overt | discrete | compact | Hausdorff | |
| ℕ×Σ | YES | NO | NO | NO |
| ℝ, ℝn | YES | NO | NO | YES |
| Σ | YES | NO | YES | NO |
| I, 2ℕ | YES | NO | YES | YES |
| free combinatory algebra | YES | YES | NO | NO |
| ℕ, ℚ | YES | YES | NO | YES |
| Kuratowski finite | YES | YES | YES | NO |
| finite (n) | YES | YES | YES | YES |
| the set of codes of | ||||
| non-terminating programs | NO | YES | NO | YES |
The axioms only provide the quantifiers ∀∅≡⊤, ∃∅≡⊥, ∀2≡∧, ∃2≡∨ and ∃ℕ directly — it is the business of this paper to construct ∃ℝ, ∃I and ∀I, in Sections 9 and 10. To put this the other way round, assuming that a future extension of the calculus will allow arbitrary nesting of ⇒ and ∀ in statements (cf. Remark 4.6), these constructions will justify quantifier elimination in the corresponding cases.
The calculus as we have described it so far will be used to define individual Dedekind cuts in Section 6.


