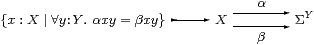
Equideductive Categories and their LogicPaul Taylor |
This is the first paper in a new programme called Equideductive Topology that, like Abstract Stone Duality, is intended to to re-axiomatise general topology in an inherently computable way. Whilst ASD characterised computably based locally compact spaces, the leading concrete model of equideductive topology is the category of sober topological spaces.
See the Prologue for a general introduction to the equideductive topology programme. If you have followed my earlier work on either the foundations of ASD or its applications to real analysis you may also like to read my 2009 Prospectus about the motivations for the new programme.
This first paper studies the interaction between equalisers and exponentials, justifying the notation
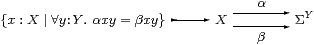
for an equaliser targeted at an exponential in an enclosing CCC.
Categorically, such subspaces are characterised as “partial products”. The logic is a kind of predicate calculus with ∀, ⇒ and & whose object language is the sober λ-calculus. The equivalence between these two formulations is proved.
It is also possible to define a weak existential quantifier in this logic. This agrees with the epis in the category, which form a factorisation system together with the partial product inclusions.
This work is intended as an alternative to Subspaces in ASD for the foundations that are needed for the applications of ASD.
Download the paper to print it
PDF, DVI, compressed PostScript or A5 booklet.
This document was translated from LATEX by HEVEA.