


In order to put some topological flesh on this categorical skeleton, we need some more specific ideas about the object Σ. Beware that, in other subjects, Σ need not be a two-element set or a subobject classifier (cf. §4.3). In fact, we shall see that one should instead view it as the space that corresponds under Stone duality to the free algebra on one generator.
7.1.
We have already made use of the analogy between topology and set theory,
in the form of the Lindenbaum–Tarski–Paré theorem
in §§4.5 & 5.3, as part of the motivation of
the monadic property as an abstract formulation of Stone duality.
Similarly, we begin by looking at the subobject classifier
(lattice of truth-values) Ω in a topos,
in order to identify the relevant properties of its analogue in topology.
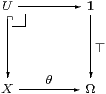
The defining property is that any subobject U↪ X is the inverse image of ⊤:1↪Ω along some unique map θ:X→Ω. That is, there is a pullback

The map θ is called the classifier, and it is crucial that isomorphic subspaces correspond to equal classifiers.
7.2.
Relying on this, if we are able to show that two constructions yield
equivalent subobjects then the corresponding classifying maps are equal.
Stripping out all extensional ideas, this means that we regard
two propositions φ and θ as equal if they are
inter-provable.
Any proof is as good as any other,
in contrast to the view of many type theorists,
who regard different proofs of the same proposition
as terms of an analogous type (cf. §2.2).
Although individual propositions are not regarded as types in topos theory, the type Ω is that of all propositions. Treating it as an object like any other means that we are doing higher order logic. There are some strange consequences of the translation of inter-provability into equality, since functions of a logical argument must respect equality.
In particular, to assert any ω (where ω∈Ω) is the same as to say that ω is equal to ⊤, from which it follows that Fω=F⊤ for any function F:Ω→Ω. Now, this equality means that Fω⇒ F⊤ and Fω⇐ F⊤, still under the hypothesis ω. But ω quā hypothesis may be eliminated using Gentzen’s introduction rule for ⇒ (cf. §2.1), in the form
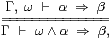
|
giving ω∧ Fω⇒ F⊤ and Fω⇐ω∧ F⊤. From these we deduce the Euclidean principle,
| for any F:Ω→Ω and ω:Ω, ω∧ Fω ⇔ ω∧ F⊤. |
We shall see that this is more than just a curiosity of higher order logic.
7.3.
In a topos, Ω classifies arbitrary subobjects,
but Giuseppe Rosolini refined the definition to handle restricted
classes of monos in other kinds of categories,
such as open subspaces in topology and recursively enumerable subsets
in the theory of computability.
The class of monos, which he called a dominion, must include
all isomorphisms and be closed under composition and under pullback
along arbitrary maps.
Then a dominance ⊤:1→Σ has the same definition
as Ω, but restricted to the given class of monos
[Ros86].
The Euclidean principle holds for any dominance Σ of which
all powers ΣX exist, not just for Ω in a topos,
as is shown diagrammatically in [C].
We shall prove the converse in §8.4
and recover the topos situation in §9.3.
7.4.
Now consider the Sierpiński space in classical topology.
This has two points, ⊤ and ⊥,
of which the former is open and the latter closed, like this:
|
| . |
According to our stated methodology, we employ this space because of its universal property. This says that there is a three-way bijective correspondence amongst
where we shall say that θ classifies U≡θ−1(⊤) and co-classifies C≡θ−1(⊥). Diagrammatically, these inverse images are given by the two pullbacks
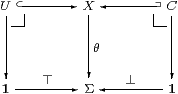
Either of the subobjects U or C determines θ (and so the other subobject) uniquely, so open inclusions form a dominion for which ⊤:1→Σ is a dominance, whilst closed inclusions form another dominion for which ⊥:1→Σ is a dominance.
7.5.
It is very difficult to assess the significance of a classical statement
about the two-element set (cf. §3.4)
,
so once again we turn to locale theory for a constructive view.
An “open subspace” of a locale is an element of the corresponding
frame, a:1→ A, and such elements correspond bijectively to
frame homomorphisms F 1→ A.
As our candidate for the Sierpiński locale,
we therefore have the free frame F 1 on one generator
[JT84, §IV 3];
by §4.4, this is the lattice of Scott-open subsets
of ℘(1)≅Ω.
Recall from §4.8 that the open and closed sublocales of X named by a∈ A are given by the nuclei a⇒(−) and a∨(−) respectively. If b∈ A gives rise to an isomorphic sublocale of either kind then the corresponding nuclei are equal as endofunctions, but by applying them both to ⊥, a and b, we deduce that a=b. So the Sierpiński locale enjoys the same universal property as its classical analogue, cf. [Joh82, Lemma II 2.6].
7.6. Hence, in the category of locally compact locales,
the Sierpiński locale is a dominance in two ways.
It therefore satisfies both the Euclidean principle and its lattice dual.
Besides this, any endofunction F:Σ→Σ preserves the order on Σ. Putting all three of these properties together, we deduce that
| Fσ ⇔ F⊥∨σ∧ F⊤, |
which is called the Phoa principle, and had already been observed in computability theory. Indeed, Martin Hyland, who named this principle after his student Wesley Phoa (pronounced “Pwah”), emphasised that Σ should classify both RE and co-RE subsets [Hyl91].
7.7.
Once again, it is difficult to see the real meaning of such simple formulae
as the Euclidean and Phoa principles.
The latter says say that any function F:Σ→Σ
is equal to a polynomial in one variable σ
and the algebraic operations, ⊤, ⊥, ∧ and ∨.
This means that ΣΣ (the topology on the
Sierpiński space) is the free algebra F1 on one generator,
as we found in locale theory.
This suggests a generalisation to algebraic or differential geometry, that any endomorphism F:R→ R of the base ring, considered as a space in the new category, is defined by a polynomial in one variable [Koc81, I 12.3]. Another way of viewing this principle is that it is what is required to make the monad for the “symbolic” algebraic structure (such as ⊤, ⊥, ∧, ∨) agree with that of the λ-calculus (Σ(−)⊣Σ(−)).
It was in order to provoke investigation of this analogy that I gave the name Euclidean principle to the earlier equation, since it resembles one step of the Euclidean algorithm for highest common factors. If the Σ2-monad is really the fundamental idea, then the Phoa principle would say that the symbolic operations agree with it, whilst subobjects would just be a manifestation of polynomials that is peculiar to set theory and topology.
7.8.
In the next section we shall add the Phoa
principle to the monadic calculus from §6,
and prove some results from it that look a lot like the
familiar properties of open, closed and compact subspaces.
Of course, this indicates that the intuitions that we have
considered so far are sound and substantial.
What’s surprising is how much can be done in the absence of an axiom that actually states general Scott continuity (§11). One might expect this to be essential for topology, especially considering its fundamental role in the applications in computer science since Scott’s original work in the 1970s.
Even though the theory at this second stage is manifestly incomplete, it is worthy of study as it stands, because it is still fully lattice dual. We can rewrite any theorem by interchanging (all of) the following symbols or concepts with their partners, and obtain another valid theorem:
| ⊑ | ⇒ | ⊤ | ∧ | ∃ | = | open | discrete | ? | open | |
| ⊒ | ⇐ | ⊥ | ∨ | ∀ | ≠ | closed | Hausdorff | compact | proper |
In particular, in §8.5 we shall have a proof rule that looks like Gentzen’s for classical ¬, alongside the one in §§2.1 & 7.2 for ⇒. The “classical” rule is valid constructively (in particular, in intuitionistic locale theory, §7.5) because it says the same thing for inclusions of closed subspaces that the “intuitionistic” rule says about open ones. Open and closed subspaces are related via their common classifiers (§7.4), and not by set-theoretic complementation. Statements in ASD are therefore free of the double negations that plague mathematics based on intuitionistic set theory, whether they are written in a categorical or type-theoretic style.
7.9.
Symmetries like this in a theory are powerful
because they are predictive.
(Consider Mendeleev’s periodic table,
or Dirac’s relativistic quantum mechanics.)
When we pair up concepts with their duals,
we often find that some things were missing.
(New elements or particles, such as the positron.)
What is the counterpart of compactness in the table above? Since the symbolic form of one topological concept is the universal quantifier (§5.7), the missing idea must be given by the existential quantifier.
Turning to locale theory for more inspiration, a compact locale is one whose terminal projection K→1 is proper, so we are looking for those for which this map is open, and indeed they were studied in [Joh84, JT84] and called open locales. Bourbaki spaces throw no light on this property, because they all have it. Casting our philosophical net a little wider, however, we find analogous ideas in computability theory (recursive enumerability) and constructive analysis (locatedness [Spi10]). The common theme seems to be an explicit presentation of something.
However, when we look at subspaces that are “open” in this sense, it turns out that they are often (but by no means always) closed subspaces, so we need another word for the idea. In English, the word overt means “open” in its sense of being explicit, so it captures these ideas very well, although it is a little difficult to find appropriate translations into other languages.
Bourbaki spaces and locales treat infinitary unions and finitary intersections asymmetrically. This is explained in ASD by saying that we may form joins indexed by overt objects and meets by compact ones.


