


By the monadicity property, our category has finite coproducts, indeed ΣX+Y≅ΣX×ΣY. In this section we consider the question of whether these coproducts are stable and disjoint, and investigate the consequences of assuming that particular objects are overt.
[Theorem B 11.8 constructs coproducts of general spaces in the category and shows that they are stable and disjoint, just assuming that Σ has a point.]
Proposition 9.1
Proof [b] is Corollary 8.4. To see α∧(β∨γ)⇔ (α∧β)∨(α∧γ) directly from the Euclidean principle, consider F(σ)≡ (σ∧β)∨(σ∧γ). [d] is Proposition 9.5 below. ▫
So for this section we shall assume that Σ is a distributive lattice. We shall not use the dual Euclidean principle or monotonicity, so the results are applicable to elementary toposes. The main one says that, in the coproduct of spaces, the two components are embedded as complementary open subsets. The coproduct is therefore stable and disjoint, and the empty space is strict.
Theorem 9.2
The category C is extensive, i.e. it has stable disjoint coproducts
[Coc93, CLW93] [Tay99, §5.5],
cf. [JT84, Corollary to V 2 1] for locales.

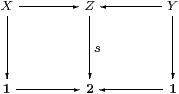
Proof Given any commutative diagram in C as shown above, we must show that the top row is a coproduct of spaces (Z=X+Y) iff the squares are pullbacks (inverse images). We do this by considering the corresponding diagram of algebras, with A≡ ΣX, B≡ ΣY and C≡ ΣZ.
First, let φ≡ Σs(⊤,⊥),ψ≡ Σs(⊥,⊤)∈ C. Since Σ is a lattice and Σs is a homomorphism, φ∧ψ⇔ ⊥ and φ∨ψ⇔ ⊤ in C. The definition of φ makes the diagram
commute, in which the square rooted at 2 is a pullback iff that at Σ is one.
Now suppose that Z=X+Y, so C=A× B. Then φ≡ (⊤,⊥)∈ A× B and C↓φ≡ (A× B)↓(⊤,⊥)≅ A. This means that X≅[φ], i.e. the square rooted at Σ is a pullback, whence so is that at 2.
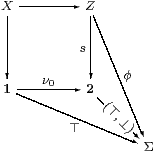
Conversely, suppose that the two squares are pullbacks, so X=[φ] and Y=[ψ]. Then
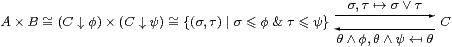
is an isomorphism because, using distributivity,
| (θ∧φ)∨(θ∧ψ) = θ∧(φ∨ψ) =θ∧⊤ =θ |
| (σ∨τ)∧φ = (σ∧φ)∨(τ∧φ) =σ∨⊥ =σ |
since σ⊑φ and τ∧φ⊑ψ∧φ=⊥. ▫
Remark 9.3
The category of stable predomains
(i.e. of disjoint unions of stable domains, Example 4.5)
is also extensive,
because the forgetful functor to Set creates coproducts and pullbacks
(in the category, not the domains).
We may also see this by a version of the preceding argument,
since it only depends on being able to define φ∨ψ
when φ and ψ are disjoint (φ∧ψ=⊥):
in terms of the systems of icicles that they classify,
to construct φ∨ψ,
each φ-icicle must be either wholly contained in a single ψ-icicle,
or wholly disjoint from them, and vice versa.
Nevertheless, Σ is not an internal lattice
— even classically, where it has only two points. ▫
Proposition 9.4
If X and Y are both overt or both compact then so is X+Y.
If f1:X1→ Y1 and f2:X2→ Y2 are both pre-open or both pre-proper maps, then so is f1+f2:X1+X2→ Y1+Y2.
Proof We define
| ∃X+Y: ΣX+Y≅ΣX×ΣY→Σ×Σ→Σ by (φ,ψ)↦ (∃ x.φ x)∨(∃ y.ψ y), |
∀X+Y by (∀ x.φ x)∧(∀ y.ψ y) and ∃f1+f2 by ∃f1×∃f2: ΣX1×ΣX2→ΣY1×ΣY2.
The adjunction and Frobenius laws hold componentwise. ▫
Proposition 9.5
If X and Y are both discrete or both Hausdorff then so is X+Y.
Proof The decomposition in the diagram depends on distributivity, but to recover X+Y as the fourfold coproduct [=X]+[⊥]+[⊥]+[=Y] also requires that coproducts be stable and disjoint.
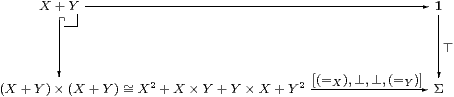
Similarly (≠X+Y) is given by [≠X,⊤,⊤,≠Y]. ▫
Proposition 9.6 Assuming the dual Euclidean principle,
any subset U that is both open and closed is
a component of a disjoint union as in Theorem 9.2.
Proof Let U≡ φ−1(⊤)=ψ−1(⊥) and put V≡ φ−1(⊥) and W≡ ψ−1(⊤), so
| 0=U⋂ W=(φ∧ ψ)−1(⊤) 0=V⋂ U=(φ∨ ψ)−1(⊥). |
By uniqueness of characteristic maps of both kinds, φ∧ ψ=⊥ and φ∨ ψ=⊤, so we have the situation of Theorem 9.2, V≡ W being the complement of U. ▫
In a non-Boolean topos, by contrast, a subset that is both open and closed in our sense need not be complemented, but merely ¬¬-closed.


