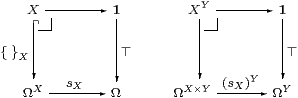



This section characterises the case where ℰ is an elementary topos and Ω its subobject classifier [Joh77, Chapter 1] [BW85, Chapter 2]. We change the notation from (C,Σ) to (ℰ,Ω) to emphasise that this is the only section of the paper in which we either assume directly that ℰ is a topos (and Ω classifies all monos) or make other assumptions that turn out to be equivalent to this.
In the earlier parts of this paper we have tried to generalise as much as possible of the basic theory of elementary toposes from higher order to geometric logic, i.e. from Set and toposes to LKLoc and abstract Stone duality. We begin this section with a proof of Paré’s theorem. The reason for doing this is to show what (little) remains that is peculiar to the topos case, and apparently cannot be generalised. [Equideductive topology also incorporates the ideas of Lemmas 11.9 and 11.11 below into topology, so even less remains that is peculiar to the topos case.] Some further simplifications could be made with the aid of the theory of replete objects [BR98], and we switch notation back to Σ for some parts of the present argument that can easily be generalised.
We conclude with a “converse” of Paré’s theorem: a new characterisation of elementary toposes that is not based on the notion of subset.
Definition 11.1 An elementary topos is a category ℰ
with an exponentiating classifier Ω as in Section 2,
but for all monos.
In particular,
since X↪ X× X is classified, all objects are discrete,
so all equalisers and pullbacks exist by Proposition 10.1.
Bill Lawvere and Myles Tierney originally included finite limits and cartesian closure in the definition [Law71], but these conditions are redundant.
Remark 11.2 Anders Kock [KM74]
constructed function-types
by applying (−)Y to the pullback square on the left:
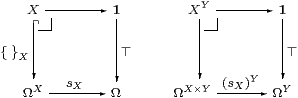
where { }X is mono by Lemma 6.12 and sX(φ) says that φ is a singleton5. Appealing though this observation is for its directness, it is only applicable to the topos situation, where { }X is open. Corollary 11.5 is available more generally.
Kock’s student and co-author Christian Mikkelsen constructed finite colimits using the minimal topos axioms. However, their existence follows much more easily from the next result, due to Robert Paré [Par74], which was the inspiration for the present work. (It is reproduced in Mikkelsen’s thesis, [Mik76, p. 57].) Nevertheless, Mikkelsen’s characterisation of X+Y⊂ΩX×ΩY is much simpler than the one obtained by unwinding the monadic result: [Tay99] uses it in Example 2.1.7, before defining categories in Section 4.1 and monads in Section 7.5.
Theorem 11.3 For a topos,
Ω(−)⊣Ω(−) is monadic.
Proof Since every object X is discrete, ηX is mono by Lemma 6.12, so Ω(−) is faithful [Mac71, §IV 3]. But as ηX is classified (open), it is regular mono, so Ω(−) also reflects invertibility (and X is replete in the sense of synthetic domain theory).
We know that the equaliser
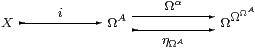
exists in any topos (since ΩΩΩA is discrete), but we need to show that Ωi is also the coequaliser. In fact, there is a split coequaliser diagram with ∃ηΩA as the other map.
Since ΩηA·ηΩA=ΩηA·Ωα=idΩA (it is called coreflexive), the square on the left is a pullback:
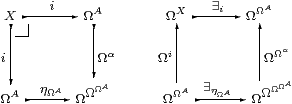
As i and ηΩA are mono, they’re open and admit existential quantification satisfying the Beck–Chevalley condition on the right. This says that Ωi and ∃i split the idempotent ΩΩα·∃ηΩA, since also Ωi·∃i=id. This idempotent is the one that arises from the split coequaliser diagram, since ΩηΩA·∃ηΩA=id and Ωα· i=ηΩA· i. Hence, by Beck’s theorem, the adjunction is monadic. ▫
Remark 11.4 In the monadic situation,
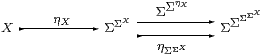
is always an Σ-split equaliser. What is peculiar to the topos case is that the quantifiers exist and are splittings. In fact the universal quantifier could be used instead, and these are the least and greatest splittings:
| ∃ηX ⊑ ηΩX ⊑ ∀ηX ∃ηΩΩX ⊑ ΩΩηΩX ⊑ ∀ηΩΩX |
The dual of the Euclidean principle is not needed to use the universal quantifier, since the argument is based on the Beck–Chevalley condition rather than the Frobenius law, cf. Proposition 3.11.
Corollary 11.5 Any topos ℰ is cartesian closed.
Proof Since it is a right adjoint, (−)Y preserves equalisers. More precisely, we first construct the equaliser
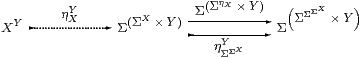
(since all finite limits exist in ℰ), and then a little easy diagram chasing shows that it also has the required universal property of the exponential. ▫
Conjecture 11.6 If all ηX are open inclusions then ℰ is a topos.
(If ∃η1 exists then negation is definable;
if ∀η1 exists then implication appears to be definable.)
Now we shall look for a converse to Paré’s theorem, i.e. given a monadic category, what further conditions would force it to be an elementary topos? These conditions will be in the form of the existence of quantifiers in higher order logic.
Lemma 11.7 The object Ω is discrete iff
it is an internal Heyting algebra.
Proof Define x=Ωy as usual by (x⇒ y)∧(y⇒ x), and conversely x⇒ y by ((x∧ y)=Ωx). ▫
Although it follows that all powers of Ω are Heyting algebras, (⇔):ΩX×ΩX→ΩX has the wrong type to be the equality predicate.
Proposition 11.8 Every object of a topos is compact,
i.e. it has a universal quantifier.
[We do not mean the sense of Dubuc and Penon [DP86],
which also requires the dual Frobenius law.]
Proof By Proposition 7.10, since the singleton {λ x.⊤}⊂ΩX is classified. ▫
Lemma 11.9 If Ω is discrete and ΩX is compact then
ΩΩX is also discrete.
Proof Leibnizian equality: F=ΩΩXG iff ∀φ:ΩX. Fφ=ΩGφ. ▫
Lemma 11.10 If X is T0
(i.e. ηX:X→ΩΩX is mono)
and ΩΩX is discrete then X is also discrete.
Proof Proposition 6.11. ▫
There is another famous reduction amongst quantifiers in higher order logic:
Lemma 11.11 If Ω is discrete and
both Ω and X are compact then X is overt.
Proof ∃ x.φ[x] is ∀σ.(∀ x.(φ[x]⇒σ))⇒σ. ▫
Theorem 11.12 Let Ω be a Euclidean semilattice in a category ℰ
such that the adjunction Ω(−)⊣Ω(−) is monadic.
Then the following are equivalent:
Hence ℰ is also a pretopos and cartesian closed.
Proof [a⇒d] Proposition 11.8; [d⇒c] Lemma 11.11; [c⇒b] Lemma 11.10.
[b⇒a] Condition (b) says that the pretopos of overt discrete objects that we discussed in the previous section is in fact the whole of ℰ. Hence all maps are open (Lemma 10.2), and in particular Ω classifies all monos by Theorem 3.10 and Corollary 10.3, so ℰ is a topos. ▫
Remark 11.13 From this point of view, CDLatop falls short of being a topos
in that Υ is not discrete,
but the discrete objects are sets
(Examples 2.12 and 6.14). ▫
Putting this Theorem together with Theorem 4.2 and Remark 4.3, we have justified the claim that the monadicity property plays the role of comprehension, in the sense that it provides a new formalism for elementary toposes that makes no mention of subsets, and doesn’t even need dependent types.
Corollary 11.14
The free category with an exponentiating Heyting algebra,
such that the adjunction is monadic, all objects are overt and
all algebras are compact, is a topos.
[This suffers from the same error as Theorem 4.2.] ▫
Remark 11.15
In terms of our common formulation of geometric and higher order logic,
we have seen that the difference between them
is measured by the availability of quantifiers of various kinds.
I feel that some of these quantifiers
(in particular ∀ΩX:ΩΩX→Ω,
from which we deduced discreteness of ΩΩX)
take the atomic theory of matter beyond what is justified by
our intuition of “collections” and other mathematical objects
(such as Abelian groups with bases of formal triangulations,
from which homology and category theory developed).
Whilst a great deal of the geometrical core of mathematics could potentially be developed within our geometric logic, there are some things that cannot be done in this logically weak scheme, notably questions of well-foundedness, termination, strong normalisation and consistency in recursion theory and proof theory. We might try to formulate an intermediate scheme of quantifiers to handle these matters, retaining the Euclidean and monadic conditions as the basic framework.
At first sight, the above results would appear to rule this out, if ⇒ is to be allowed and ∀ΩX forbidden, but something similar to the latter is to be included. However, synthetic domain theory has already shown that a model may have two objects, Σ and Ω, classifying weaker and stronger fragments of logic (Remark 2.13). The extra quantifier could make use of both objects, but since all maps Ω→Σ are constant, we are left with
| ∀:ΠΣX—→Π, |
where Π is the name of the intermediate classifier, with Σ⊂Π⊂Ω. We might hope to use it to give a synthetic proof of the general recursion theorem, that the induction scheme suffices for recursion [Tay99, §6.3].
But what is already clear from these investigations is that our “synthetic” arguments in topology are much simpler and to the point than the traditional ones in point-set topology, locale theory and continuous lattices. So long as we give up trying to detect equality of predicates, they also have a programming interpretation.
Acknowledgements. The original inspiration for this work came while I was visiting Pino Rosolini at the Università degli Studi di Genova in March 1993, and many of the results were found during my second visit in October and November 1997; both visits were funded by the Italian Concilio Nazionale della Ricerca.
This paper was drafted during my visit to Macquarie University in August 1997.
The work has benefitted much from my discussions with Martín Escardó, Martin Hyland, Peter Johnstone, Anders Kock, Eugenio Moggi, Bob Paré, Bob Rosebrugh, Pino Rosolini, Andrea Schalk, Alex Simpson, Thomas Streicher, Steve Vickers, Graham White, Todd Wilson and Richard Wood.
The Euclidean principle was announced in the categories electronic mail forum on 29 June 1997, but I had first encountered this equation on 12 March 1997.


