| (x<maxK) | ⇔ | (∃ k:K.x< k) |
| (maxK< x) | ⇔ | (∀ k:K.k< x) |
| k:K | ⊢ | k≤maxK |
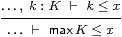



The combination of overtness and compactness is extremely powerful in constructive topology, as we shall see in the remainder of the paper. These concepts are defined by modal operators ▫ and ◊ that are expressions of type ΣΣℝ satisfying the mixed modal laws in Proposition 2.16. Since ▫ and ◊ may involve parameters, the maximum of the subspace that they define will also be an expression in the same parameters.
We begin by showing that the mixed modal laws characterise the situation in which a closed subspace of a Hausdorff space is both overt and compact.
Proposition 12.1
Let (▫,ω) define a compact subspace of a Hausdorff space H,
and let ◊ be another operator on H such that ◊ω⇔⊥
and ◊(φ∨ψ)⇔◊φ∨◊ψ.
Then ▫ and ◊ always satisfy
| ▫φ∧◊ψ=⇒◊(φ∧ψ) |
and the three subspaces have ◊⊂ω=▫ in the sense that (cf. Definition 7.17)
| λφ.φ a ⊑ ◊ ⊢ ω a⇔⊥ ⊣⊢ ▫⊑ λ φ.φ a. |
The operators also obey the other mixed law
| ▫(φ∨ψ) =⇒ ▫φ∨◊ψ |
iff (◊,ω) define a closed overt subspace, i.e. they satisfy relative instantiation,
| φ x=⇒ω x∨◊φ, |
and in this case all three subspaces coincide.
Proof If ▫φ⇔⊤ then ⊤⊑φ∨ω, so ψ⊑(φ∨ω)∧ψ⊑(φ∧ψ)∨ω. Hence
| ▫φ⇔⊤ ⊢ ◊ψ =⇒◊((φ∧ψ)∨ω) =⇒◊(φ∧ψ)∨◊ω =⇒◊(φ∧ψ), |
giving the first modal law by Axiom 5.6. Assuming the other,
| φ x∧▫⊤ =⇒▫(λ y.φ x) =⇒▫(λ y.x≠ y∨φ y) =⇒▫(λ y.x≠ y)∨◊φ ≡ ω x∨◊φ |
by Proposition 5.8 and Lemma 5.9. Conversely, by Definitions 8.1 and 11.1,
|
and again Axiom 5.6 gives the modal law. The closed and compact subspaces are equal by Proposition 8.7, and they contain or agree with the overt one by Proposition 11.6. ▫
Corollary 12.2
Let ◊ and ▫ be any terms of type ΣΣH
for a Hausdorff space H, and put ω x≡▫(λ y.x≠ y).
Then (▫,ω) and (◊,ω) satisfy
Definitions 8.1 and 11.1 iff
| ▫⊤⇔⊤ ◊ω⇔⊥ and ▫(φ∨ψ) =⇒ ▫φ∨◊ψ, |
the last being equivalent to relative instantiation, φ x⇒ω x∨◊φ.
Proof [⊢] The definitions and Propositions 8.2 and 11.2 give the first two equations and relative instantiation.
[⊣] The backward directions of the two definitions are ◊ω⇔⊥ and
| ⊤=φ∨ω ⊢ ⊤ =⇒ ▫(φ∨ω) =⇒ ▫φ∨◊ω =⇒ ▫φ. |
Forwards, we are given relative instantiation for ◊, whilst for ▫ we have
|
Applying the mixed modal laws in even the simplest case already has a dramatic result:
Theorem 12.3 Let K be a compact overt subspace.
Then it is decidable (Lemma 6.4) whether K is empty.
If it’s not, then it is both occupied and inhabited
(so these words mean the same thing in this case) and ▫⊑◊.
Proof If K is empty then ▫⊥⇔⊤ and ◊⊤⇔⊥, whereas if it’s occupied then ▫⊥⇔⊥ and if it’s inhabited then ◊⊤⇔⊤. These situations are complementary because
| ⊤ ⇔ ▫(⊥∨⊤) =⇒ ▫⊥ ∨ ◊⊤ and ⊥ ⇔ ◊(⊥∧⊤) ⇐= ▫⊥ ∧ ◊⊤. |
Also
| ▫φ ⇔ ▫(⊥∨φ) =⇒ ▫⊥∨◊φ ⇔ ◊φ, |
or
| ▫φ ⇔ ◊⊤∨▫φ =⇒ ◊(⊤∨φ) ⇔ ◊φ. |
Conversely, ▫⊑◊⊢▫⊥⇒◊⊥≡⊥ and ⊤≡▫⊤⇒◊⊤. ▫
Remark 12.4 The dichotomy is in the strict logical sense,
of which the topological manifestation (cf. Remark 4.6)
is that the parameter space Γ is a disjoint union of two clopen
subspaces, not just of an open and a closed one.
Therefore, if Γ is connected, for example if Γ≡ℝn,
something in this short argument has to break at any singularities.
As we saw informally in Proposition 2.15, it is the modal law ▫(φ∨ψ)⇒▫φ∨◊ψ that we lose, together with relative instantiation, φ x⇒ω x∨◊φ. Even in this singular case, Proposition 11.6 still ensures that any member or accumulation point of ◊ belongs to the closed subspace co-classified by ω.
Recall from Lemma 6.4 that clopen subspaces correspond to maps H→2.
Lemma 12.5 Any clopen subspace of a compact overt space X
is also compact overt, with
| ▫θ ≡ ∀ x:X.θ x∨ω x and ◊θ ≡ ∃ x:X.θ x∨α x, |
where α and ω are the given complementary open subspaces.
Proof Theorem 8.15 linked ▫ and ω. Then θ⊑ω ⊣⊢ θ∧α=⊤ ⊣⊢ ◊θ⇔⊤. ▫
Notation 12.6 Now we are ready to consider the central question about
which subsets of ℝ have suprema as Euclidean real numbers.
Classically, any non-empty subset K⊂ℝ that
has an upper bound has a least one.
In that setting, there would be no loss of generality in stating
this only when K is also closed and bounded below, i.e. compact.
In our calculus, we have already shown that any compact subspace K has a supremum, but in general this is only a descending real number (Proposition 9.13). On the other hand, any overt subspace also has a supremum, but this is an ascending real (Proposition 11.18). These define
| δ d ≡ ◊(λ k.d< k) and υ u ≡ ▫(λ k.k< u) |
in terms of ◊ and ▫. If K is empty, these definitions give
| max∅ ≡ −∞ ≡ (λ d.⊥,λ u.⊤) and min∅ ≡ +∞ ≡ (λ d.⊤,λ u.⊥). |
This case is characterised positively, if perversely, by max∅<min∅, but since it is decidable, for the moment we assume that it does not apply.
The duality between overtness and compactness is reflected in a symmetry of the proof that (δ,υ) is a Dedekind cut. This result was inspired by the constructive least upper bound principle (Definition 3.7), but interpreting the quantifiers that it involves in our topological sense:
Proposition 12.7 (Andrej Bauer)
If K is non-empty then the pair (δ,υ) is a Dedekind cut.
Hence, by Axiom 6.8, there is a unique a:ℝ
such that
| (d< a) ⇔ δ d ≡ ◊(λ k. d< k) and (a< u) ⇔ υ u ≡ ▫(λ k. k< u) . |
Proof We know that δ and υ are rounded, so it remains to show that they are disjoint, located and bounded. The proofs are dual, using the mixed modal laws and ◊σ⇒σ⇒▫σ. The first also uses transitivity and the second locatedness of the order on ℝ (Axiom 4.9).
| (δ d∧υ u) ≡ ◊(λ k. d< k)∧▫(λ k. k< u) =⇒ ◊(λ k. d< k∧ k< u) =⇒ (d< u) |
| (δ d∨υ u) ≡ ◊(λ k.d< k) ∨ ▫(λ k. k< u) ⇐= ▫(λ k.d< k∨ k< u) ⇐= (d< u). |
Propositions 9.13 and 11.18 showed respectively that ∃ d.δ d and ∃ u.υ u⇔◊⊤⇔⊤. ▫
Hence K has a supremum a, but it’s better than this:
Lemma 12.8 There is a greatest element, a∈ K.
Proof By Axiom 4.9 and one of the mixed modal laws,
|
Hence a belongs to the closed subspace, and ▫φ=⇒φ a=⇒◊φ by the relative instantiation laws for ▫ and ◊. ▫
Theorem 12.9 Any overt compact subspace K⊂ℝ
is either empty or has a greatest member, maxK≡ a∈ K.
This satisfies, for x:ℝ,
|
and
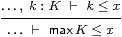
|
Proof The first two properties re-state Proposition 12.7, which also gives, for k:K,
| (maxK< k) ≡ ▫(λ k′. k′< k) =⇒ (k< k) ⇔ ⊥, |
so k≤maxK by Example 4.6. The rule on the right is obtained by substitution of maxK for k:K. ▫
Exercise 12.10
Let a,b:ℝ⇉ℝ be two functions,
so there is no question of using a case analysis
on whether a≤ b or a≥ b.
Regarding them as terms a,b:ℝ with a real parameter,
define the parametric modal operators [K] and <K> that make
the (ℝ-indexed) subspace K≡{a,b}⊂ℝ
compact and overt. Show that
| max(a,b) ≡ maxK ≡ (δ,υ) ⇔ (δa∨δb, υa∧υb). |
The properties listed in Theorem 12.9 are those for binary max in Proposition I 9.8. ▫
Corollary 12.11 Any overt compact subspace K⊂ℝ either
We therefore obtain a particular element of K⊂ℝ without using dependent choice. ▫
What can we say about where a function attains its bounds?
Proposition 12.12
Let f:X→ Y be a function between Hausdorff spaces,
and K⊂ X a compact overt subspace.
Then its image f K⊂ Y is also compact overt.
Proof We prove the modal laws in Corollary 12.2 for f K⊂ Y.
|
| ▫ |
Corollary 12.13
Any function f:K→ℝ on a non-empty compact overt space is bounded,
and attains its bounds on an occupied compact subspace Z⊂ K.
However, Z need not be overt (Example 16.15).
Proof Since the image f K⊂ℝ is an occupied compact overt subspace of ℝ, it has a maximum b∈ f K. The inverse image Z≡{x:K ∣ f x=b}⊂ K of b is compact and occupied, by Theorem 8.9. ▫
Remark 12.14
We shall see in Section 14 that,
given a polynomial equation (such as x3−x=0)
with distinct roots ({−1,0,+1}),
the argument above does indeed yield the greatest root (+1).
In the singular case, ▫ and ◊ only satisfy one of the mixed modal laws, namely the one that was used to prove disjointness of the Dedekind cut in Lemma 12.7, whilst the other law and locatedness fail. The pseudo-cut (δ,υ) nevertheless defines a compact interval [δ,υ] in the sense of Proposition 9.11, whose endpoints are the ascending real δ and the descending one υ.
For example, the polynomial equation x3+x2=0 has a stable zero at −1 and a double (unstable) one at 0, so {−1}≡ S⊂ Z≡{−1,0}. Then δ=supS=−1 and υ=supZ=0, so the interval-valued supremum of the zero set is [−1,0].
Remark 12.15
Other systems of constructive analysis prove similar results
using an idea from the classical theory of metric spaces.
A subset K is called totally bounded
if, for each ε> 0, there is a finite subset Sε⊂ K
such that ∀ x:K.∃ y∈ Sε.|x−y|<ε.
(See [SS70, Example 134.3] for a classical metric on ℝ
with a bounded subspace that is not totally bounded.)
If K⊂ℝ is closed and totally bounded, either the sets Sε are all empty, in which case K is empty too, or xn≡max(S2−n) defines a Cauchy sequence that converges to maxK [TvD88, Lemma 6.1.7].
But if we are given explicit finite sets S1, S1/2, S1/4, ..., with the above property in any compact metric space K, we may concatenate them to define a map a(−):ℕ→ K. Then ◊ψ≡∃ n.ψ an (Example 11.14) satisfies ψ x⇒◊ψ by Theorem 10.2, and hence the modal laws, so K is an overt space.
Bas Spitters has investigated how overtness is related to locatedness and other notions in constructive analysis [Spi10].
Remark 12.16
In contrast to the (infinite) subspaces of ℝ
that we have just discussed,
compact overt discrete spaces are Kuratowski-finite
(Theorem G 9.10):
they can be listed,
but it may not be possible to eliminate repetitions from a list
because equality need not be decidable [Kur20].
If such a space is also Hausdorff, i.e. its equality is decidable,
then it is finite in the usual sense, being listable without repetitions,
so we can say how many elements it has.
As in Proposition 12.1, we can use the modal operators to describe compact overt subspaces as pairs of terms. Whereas such a subspace was closed in the Hausdorff case and co-classified by ω, in the discrete case it is open (Definition 8.19) and classified by
| α x ≡ ◊(λ y.x=y), with ▫α⇔⊤. |
Moreover, there is an overt discrete space K X whose members are pairs (▫,◊) of terms that satisfy the modal laws and therefore represent Kuratowski-finite subsets of X. Hence K X is the finite powerset ℘f(X) or free semilattice. There is also an object List X that is the free monoid. The general constructions of K X and List X in [E] are rather difficult, but in the cases of X≡ℕ or ℚ, there are well known formulae for the bijections K X≅ℕ and List X≅ℕ.
These results may be used to develop combinatorial arguments such as the definition of the Riemann integral in Remark 10.12 and the results of Section 15, but it is important to appreciate that they rely on topological ideas. A list is not an indeterminate finite collection of points in a space, but a single point of a hyper-space. In order to be able to write it as a0,…,an−1 with a finite number of members (albeit possibly with repetition) and argue by induction, etc., its members have to be drawn from an overt discrete space.
This is why we insist on lists of rational numbers.
The Vietoris space of compact overt subspaces of a Hausdorff space such as ℝ is an entirely different beast, whose modal operators (called t≡▫ and m≡◊) are described for locales in [Joh82, §III.4].


