



This section shows how each new type (generated arbitrarily from comprehension and powers of products) may be expressed as a subtype (by a single comprehension) of a type in the original calculus. This is like expressing any set in Zermelo set theory as a subset of an iterated powerset, as in the von Neumann hierarchy. It will relate back to the categorical construction in Section 4, where every new object of S is a formal equaliser in S.
The structure maps in this isomorphism are, of course, terms to be defined, but they behave like the constructors i, I and admit of the comprehension calculus. That is, the lemmas that we have to prove towards this isomorphism are like the β- and η-rules of the calculus, and will therefore be presented and named as such. This is not a serious overloading of the i and I notations, as the old use has two subscripts.
Remark 9.1
Given any λ-calculus (such as ours) with all of the
usual structural rules, the corresponding category has products simply
because they are concatenations of contexts.
The problem with products
that was a central concern in the two categorical constructions
does not, unfortunately, go away so easily:
we have merely pushed it into the exponents.
A power type is Σ(−) applied to (the product of) a list of types, and λ-abstraction and application involve the list operations of push and pop (or cons and (head,tail)) on types. The normalisation process for types must therefore also deal with lists. This could be formalised by introducing meta-variables to denote either lists of types, or powers of lists. However, as this complication does not have any impact on the real issues in the argument, we leave the interested reader to carry this through for themselves, and simply consider the case of lists of length two. We take ΣY× Z to mean (ΣZ)Y, a typical term of which is λ y.φ, where y:Y and φ:ΣZ. In this sense, Σ contains the empty list.
The main technical question with products then manifests itself in this situation as the choice between IZ Y · IYZ and the other term that could serve as iΣY× Z.
Extended notation
Notation 9.2
By structural recursion on the type X, we define a type X , terms

and the idempotent EX on Σ X .
The base cases are 1, Σ and ℕ, for which
these maps are identities.
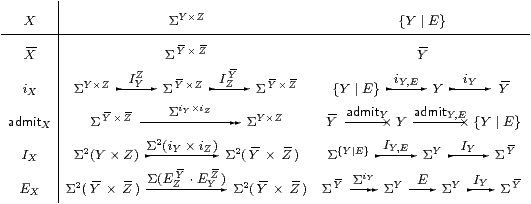 So X erases the comprehensions from X,
and iX embeds X as a subspace of X .
This has the subspace topology because of IX.
So X erases the comprehensions from X,
and iX embeds X as a subspace of X .
This has the subspace topology because of IX.
Lemma 10.10 shows that E{Y ∣ E}= E , where the translation E for terms is defined in the next section.
The normalised type
Lemma 9.3
The Σ{}η rule,
ΣiX· IX=idΣX or
φ:ΣX, x:X⊢(IXφ)(iX x)=φ x,
is valid.
Proof By structural induction on the type X. If X≡ΣY× Z then
|
If X≡{Y ∣ E} then
|
Lemma 9.4
The Σ{}β rule, IX· ΣiX=EX, is valid.
Proof By structural induction on the type X. If X≡ΣY× Z then
|
If X≡{Y ∣ E} then
|
Proposition 9.5
{ X ∣ EX} is a well formed type,
with structure iX and IX.
Proof EX on X is a nucleus (Definition 8.7), by the same argument as we used in Corollary 4.13. ▫
The other rules for the extended notation
Lemma 9.6
The {}E0 rule is well formed and
the {}E1 rule is valid.
Proof There is no issue of well-formedness, as iX at any type is built using iY,E and IY,E but not admitY,E from the comprehension calculus. Now let x:X and φ:Σ X . From Lemmas 9.3 and 9.4 we have
| ΣiX· EX = ΣiX· IX·ΣiX = ΣiX, |
so φ(iX x) = ΣiXφ x = (ΣiX· EX)φ x = EXφ(iX x) . ▫
Lemma 9.7 The {}I rule is well formed,
and the {}β rule is valid, at type X≡ΣY× Z.
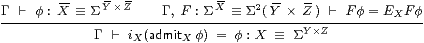
|
Proof In the introduction rule, admitXφ = ΣiY× iZφ with no issue of well-formedness, as this expression does not use admit from the comprehension calculus. Also,
|
So φ=iXadmitXφ by T0. ▫
Lemma 9.8
If X≡{Y ∣ E} then EX⊂ Y EY
in the sense of Notation 4.4.
Proof EX=E{Y ∣ E}=IY · E · ΣiY, whilst EY=IY· ΣiY by Lemma 9.4. Then
| EY· EX = IY · ΣiY · IY · E · ΣiY = IY · E · ΣiY = EX = IY · E · ΣiY · IY · ΣiY = EX · EY |
by Lemma 9.3 (Σ{}η for Y). ▫
Lemma 9.9
The {}I rule is well formed,
and the {}β rule is valid, at all types.
Proof By structural induction on the type X, with Y≡ℕ or ΣZ as the base case (even when Z is itself a product or comprehension type), so consider X≡{Y ∣ E}.
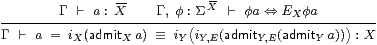
|
First, φ a ⇔ EXφ a ⇔ (EY· EX) φ a ⇔ EY φ a using the given side-condition twice, and since EX⊂EY. Hence b≡ admitY a:Y is well formed, and iY b=a by the induction hypothesis, {}β for Y.
For the whole expression to be well formed, we need ψ:ΣY⊢ψ b⇔ Eψ b. Put φ≡ IYψ:Σ Y . Then
|
Finally, iX(admitX a) = iY,E(iY(admitY(admitY,E a))) = iY,E(admitY,E a) by the induction hypothesis, but this is a by {}β for {Y ∣ E}. ▫
Lemma 9.10
The {}η rule, admitX· iX=idX, is valid.
Proof The expression is well formed by Lemmas 9.6 and 9.9. We prove the equation by structural induction on the type X. If X≡ΣY× Z then, as in Lemma 9.3,
|
If X≡{Y ∣ E} then admitX· iX = admitY,E · admitY · iY · iY,E, which is admitY,E· iY,E by the induction hypothesis, but this is id{Y ∣ E} by {}η for {Y ∣ E}. ▫
The isomorphism
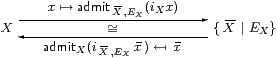
Proof For the two admit-expressions to be well formed, we need properties of the form EXφ(i x) ⇔ φ(i x), where i x is either iX x or i X ,EX x , cf. Lemma 8.10.
admit X , EX(iX x) is well formed by Lemma 9.6 ({}E1 for X) and {}I for { X ∣ EX}.
admitX(i X , EX x ) is well formed by {}E1 for { X ∣ EX} and Lemma 9.9 ({}I for X).
admitX(i X , EX(admit X , EX(iX x))) = admitX(iX x) by {}β for { X ∣ EX}, but this is x by Lemma 9.10 ({}η for X).
admit X , EX(iX(admitX(i X , EX x ))) = admit X , EX(i X , EX x ) by Lemma 9.9 ({}β for X), but this is x by {}η for { X ∣ EX}. ▫
Proposition 9.12 This induces
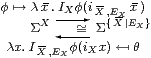
Proof φ(admitX(i X , EX x )) ⇔ IXφ(iX(admitX(i X , EX x ))) ⇔ IXφ(i X , EX x ) because of Lemmas 9.3 and 9.9 (Σ{}η and {}β for X).
θ(admit X , EX(iX x)) ⇔ I X , EXθ(i X , EX(admit X , EX(iX x))) ⇔ I X , EXθ(iX x) by Σ{}η and {}β for { X ∣ EX}. ▫


