9  Normalisation for types

This section shows how each new type (generated arbitrarily from comprehension and powers of products) may be expressed as a subtype (by a single comprehension) of a type in the original calculus. This is like expressing any set in Zermelo set theory as a subset of an iterated powerset, as in the von Neumann hierarchy. It will relate back to the categorical construction in Section 4, where every new object of S is a formal equaliser in S.

The structure maps in this isomorphism are, of course, terms to be defined, but they behave like the constructors i, I and admit of the comprehension calculus. That is, the lemmas that we have to prove towards this isomorphism are like the β- and η-rules of the calculus, and will therefore be presented and named as such. This is not a serious overloading of the i and I notations, as the old use has two subscripts.

Remark 9.1 Given any λ-calculus (such as ours) with all of the usual structural rules, the corresponding category has products simply because they are concatenations of contexts. The problem with products that was a central concern in the two categorical constructions does not, unfortunately, go away so easily: we have merely pushed it into the exponents.

A power type is Σ⁽⁻⁾ applied to (the product of) a list of types, and λ-abstraction and application involve the list operations of push and pop (or cons and (head,tail)) on types. The normalisation process for types must therefore also deal with lists. This could be formalised by introducing meta-variables to denote either lists of types, or powers of lists. However, as this complication does not have any impact on the real issues in the argument, we leave the interested reader to carry this through for themselves, and simply consider the case of lists of length two. We take Σ^{Y× Z} to mean (Σ^Z)^Y, a typical term of which is λ y.φ, where y:Y and φ:Σ^Z. In this sense, Σ contains the empty list.

The main technical question with products then manifests itself in this situation as the choice between I_Z  ^Y · I_Y^Z and the other term that could serve as i_{Σ^{Y× Z}}.

Extended notation

Notation 9.2 By structural recursion on the type X, we define a type   X , terms

and the idempotent E_X on Σ  ^X . The base cases are 1, Σ and ℕ, for which these maps are identities. 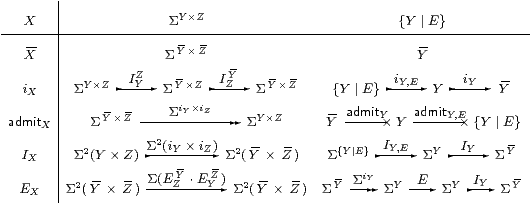So   X  erases the comprehensions from X, and i_X embeds X as a subspace of   X . This has the subspace topology because of I_X.

Lemma 10.10 shows that E_{{Y ∣ E}}=  E , where the translation   E  for terms is defined in the next section.

The normalised type

Lemma 9.3 The Σ^{}η rule, Σ^i_X· I_X=id_Σ^X or φ:Σ^X, x:X⊢(I_Xφ)(i_X x)=φ x, is valid.

Proof    By structural induction on the type X. If X≡Σ^{Y× Z} then

If X≡{Y ∣ E} then

Lemma 9.4 The Σ^{}β rule, I_X· Σ^i_X=E_X, is valid.

Proof    By structural induction on the type X. If X≡Σ^{Y× Z} then

If X≡{Y ∣ E} then

Proposition 9.5 {  X  ∣ E_X} is a well formed type, with structure i_X and I_X.

Proof    E_X on   X  is a nucleus (Definition 8.7), by the same argument as we used in Corollary 4.13.         ▫

The other rules for the extended notation

Lemma 9.6 The {}E₀ rule is well formed and the {}E₁ rule is valid.

Proof    There is no issue of well-formedness, as i_X at any type is built using i_Y,E and I_Y,E but not admit_Y,E from the comprehension calculus. Now let x:X and φ:Σ  ^X . From Lemmas 9.3 and 9.4 we have

so φ(i_X x)  =  Σ^i_Xφ x  =  (Σ^i_X· E_X)φ x  =  E_Xφ(i_X x) .         ▫

Lemma 9.7 The {}I rule is well formed, and the {}β rule is valid, at type X≡Σ^{Y× Z}.

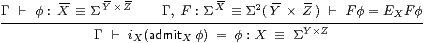
Proof    In the introduction rule, admit_Xφ = Σ^{i_Y× i_Z}φ with no issue of well-formedness, as this expression does not use admit from the comprehension calculus. Also,

So φ=i_Xadmit_Xφ by T₀.         ▫

Lemma 9.8 If X≡{Y ∣ E} then E_X⊂  _Y E_Y in the sense of Notation 4.4.

Proof    E_X=E_{{Y ∣ E}}=I_Y · E · Σ^i_Y, whilst E_Y=I_Y· Σ^i_Y by Lemma 9.4. Then

by Lemma 9.3 (Σ^{}η for Y).         ▫

Lemma 9.9 The {}I rule is well formed, and the {}β rule is valid, at all types.

Proof    By structural induction on the type X, with Y≡ℕ or Σ^Z as the base case (even when Z is itself a product or comprehension type), so consider X≡{Y ∣ E}.

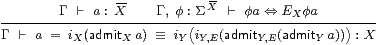
First, φ a ⇔ E_Xφ a ⇔ (E_Y· E_X) φ a ⇔ E_Y φ a using the given side-condition twice, and since E_X⊂E_Y. Hence b≡ admit_Y a:Y is well formed, and i_Y b=a by the induction hypothesis, {}β for Y.

For the whole expression to be well formed, we need ψ:Σ^Y⊢ψ b⇔ Eψ b. Put φ≡ I_Yψ:Σ  ^Y . Then

Finally, i_X(admit_X a) = i_Y,E(i_Y(admit_Y(admit_Y,E a))) = i_Y,E(admit_Y,E a) by the induction hypothesis, but this is a by {}β for {Y ∣ E}.         ▫

Lemma 9.10 The {}η rule,  admit_X· i_X=id_X,  is valid.

Proof    The expression is well formed by Lemmas 9.6 and 9.9. We prove the equation by structural induction on the type X. If X≡Σ^{Y× Z} then, as in Lemma 9.3,

If X≡{Y ∣ E} then admit_X· i_X = admit_Y,E · admit_Y · i_Y · i_Y,E, which is admit_Y,E· i_Y,E by the induction hypothesis, but this is id_{{Y ∣ E}} by {}η for {Y ∣ E}.         ▫

The isomorphism

Proposition 9.11

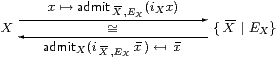
Proof    For the two admit-expressions to be well formed, we need properties of the form E_Xφ(i x) ⇔ φ(i x), where i x is either i_X x or i  _X ,EX  x , cf. Lemma 8.10.

admit  _{X , EX}(i_X x) is well formed by Lemma 9.6 ({}E₁ for X) and {}I for {  X  ∣ E_X}.

admit_X(i  _{X , EX}  x ) is well formed by {}E₁ for {  X  ∣ E_X} and Lemma 9.9 ({}I for X).

admit_X(i  _{X , EX}(admit  _{X , EX}(i_X x))) = admit_X(i_X x) by {}β for {  X  ∣ E_X}, but this is x by Lemma 9.10 ({}η for X).

admit  _{X , EX}(i_X(admit_X(i  _{X , EX}  x ))) = admit  _{X , EX}(i  _{X , EX}  x ) by Lemma 9.9 ({}β for X), but this is   x  by {}η for {  X  ∣ E_X}.         ▫

Proposition 9.12 This induces    

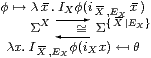
Proof    φ(admit_X(i  _{X , EX}  x )) ⇔ I_Xφ(i_X(admit_X(i  _{X , EX}  x ))) ⇔ I_Xφ(i  _{X , EX}  x ) because of Lemmas 9.3 and 9.9 (Σ^{}η and {}β for X).

θ(admit  _{X , EX}(i_X x)) ⇔ I  _{X , EX}θ(i  _{X , EX}(admit  _{X , EX}(i_X x))) ⇔ I  _{X , EX}θ(i_X x) by Σ^{}η and {}β for {  X  ∣ E_X}.         ▫