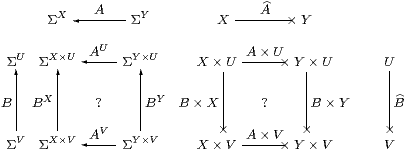
commute. Hence × is a symmetric monoidal structure in the category whose objects are those of S and whose morphisms A:X−× Y are the A that preserve ⊤ and ∧, cf. Section A 3. In particular, these maps commute with ∀K, for any compact K.



Making use of the availability of bases for all definable objects, this section establishes the basic properties that justify the claim that abstract Stone duality is an account of domain theory and general topology, at least in so far as its morphisms are continuous functions. We first prove something that was claimed in Remark 4.8.
Proposition 9.1
Let M be an overt discrete object with effective basis
(βn,An) indexed by an overt discrete object N.
Then M is the subquotient of N by an open partial equivalence relation.
Proof Write n⊩ x for n:N, x:M ⊢ An{x}∧ βn x (using discreteness of M) and N′={n ∣ ∃ x.n⊩ x}⊂ N, which is open, using overtness.
Then, using the basis expansion of open {x},
| ⊤ ⇔ (x=M x) ⇔ |
| (x) ⇔ ∃ n.An |
| ∧βn x ⇔ ∃ n.n⊩ x, |
so every point x:M has some code n:N′. The latter belongs only to x since
|
Hence N′→ΣM by n↦λ x.n⊩ x factors through {}:M↣ΣM, and M is N/∼ where (m∼ n)≡(∃ x.m⊩ x∧ n⊩ x) [C]. ▫
We leave it as an exercise to define partial equivalence relations on List (N) whose quotients are List (M) and K(M).
Corollary 9.2 Every definable overt discrete object
is a subquotient of ℕ by an open partial equivalence relation. ▫
This does not restrict how “big” overt discrete objects can be in general models of ASD: for example, ℵ1 still belongs to the classical model. It simply says that, having required certain base types to be overt discrete, as we did with ℕ in Axiom 4.4, the additional overt discrete objects that can be constructed from them are no bigger.
Corollary 9.3 In the free model, if an object X has a basis indexed by any
overt discrete object M then it has one indexed by ℕ.
Proof Let n:ℕ, m:M⊢ n⊩ m be the relation defined in the Proposition and (βm,Am) the basis on X. Define
| γn ≡ λ x.∃ m.n⊩ m∧βm x and Dn ≡ λφ.∃ m.n⊩ m∧ Amφ. |
So γn=βm and Dn=Am if n⊩ m, but γn=⊥ and Dn=⊥ if n∉ N′. Then, using the properties of ⊩, (γn,Dn) is an effective basis because
|
The next goal is Scott continuity, i.e. preservation of directed joins. Recall from Definition 4.13 that these are defined in terms of a structure (S,0,+) that indexes two families
| s:S ⊢ αs:Σ and φs:ΣX. |
Lemma 9.4 Γ, ℓ:Fin(M) ⊢
(∀ m∈ℓ.∃ s:S.αs∧φs m) ⇔
(∃ s:S.αs∧∀ m∈ℓ.φs m) .
Proof We have to show ⇒, as ⇐ is easy. For the base case, ℓ≡ 0, put s≡ 0. For the induction step, ℓ′=m::ℓ, suppose by the induction hypothesis that
| αt∧φt m ∧ αs∧∀ m∈ℓ.φs m |
Put u≡ s+t:S, so αu⇔αs+t⇔αs∧αt and φs,φt≤φu, so we have αu∧∀ m∈m::ℓ.φu m.
This proof is for lists, but a similar induction scheme works for subsets too, cf. [Tay99, Section 6.5]. Since this equational hypothesis is of the form σ⇔⊤, it can be eliminated in favour of an open subobject of the context [E, §2]. ▫
Lemma 9.5
Any Γ⊢F:Σ3 N preserves the directed join
Γ⊢∃ s.αs∧ Φs:ΣΣN.
Proof Using the previous lemma for X≡ ΣN and M≡Fin N,
|
Theorem 9.6 Any Γ⊢ F:ΣΣX
preserves the directed join ∃ s.αs∧φs:ΣX.
Proof Making the same substitutions as in Lemma 8.10,
|
Corollary 9.7 All F:ΣY→ΣX preserve directed joins. ▫
We can now see the construction in Lemma 8.10 as a composite, of Lemma 8.4 twice and the following result. In order to apply F:ΣΣX to the basis decomposition of φ:ΣX, the decomposition must be a directed join.
Lemma 9.8 If X has a ∨-basis then
ΣX has a prime ∧-basis.
Proof For F:ΣΣX and φ:ΣX, since the ∨-basis gives a directed join,
| Fφ ⇔ F(∃ n.Anφ∧βn) ⇔ ∃ n.Anφ∧ Fβn. |
This is the decomposition of F with respect to the prime ∧-basis with
| Bn ≡ An and An ≡ λ F.Fβn. |
Notice that it reverses the imposed order on the indexing object. ▫
We can also go up to the second exponential with just one level of lists.
Lemma 9.9 Let (βn,An) be a ∨-basis for X.
Then
| Bℓ≡λ F.∀ n∈ℓ.Fβn and Aℓ≡λF.F(λφ.∃ n∈ℓ.Anφ) |
define a prime ∧-basis for ΣΣX, i.e. we have a basis decomposition
| F:Σ3 X ⊢ F = λ F.∃ℓ. F(λφ.∃ n∈ℓ.Anφ)∧∀ n∈ℓ.Fβn. |
Proof (An,λ F.Fβn) is a basis and (λφ.∃ n∈ℓ.Anφ, λ F.∀ n∈ℓ.Fβn) an ∨-basis for ΣX by Lemmas 9.8 and 8.4. Finally, Lemma 9.8 gives the prime ∧-basis for ΣΣX. ▫
As a corollary, we have another result similar to Corollary 9.2, although this one does restrict the size of overt discrete compact objects. Such objects are called Kuratowski finite: see [E] for more detail. Beware that even finiteness is not the same as being a numeral, for example a Möbius band has a finite set of edges that is locally equal to 2, but this set is not a numeral.
Theorem 9.10
An object N is overt discrete compact iff it is listable,
and therefore a quotient of a numeral by an open equivalence relation.
Proof Expanding the quantifier ∀N using the filter ∨-basis for N indexed by List N,
| ∀Nφ ⇔ ∃ℓ.∀ n.n∈ℓ∧∀ m∈ℓ.φ m, |
so ⊤⇔∀N⊤⇔∃ℓ.∀ n.n∈ℓ. The numeral is (the length of) ℓ, though we require the Existence Property (cf. Remark 4.11) to pin down its order and so make it a quotient of a numeral. ▫
As another corollary, we can complete the business of Proposition 5.11 and Lemma 8.2.
Theorem 9.11 Let A:ΣY→ΣX and B:ΣV→ΣU.
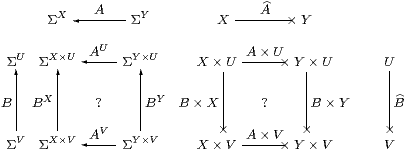
commute. Hence × is a symmetric monoidal structure in the category whose objects are those of S and whose morphisms A:X−× Y are the A that preserve ⊤ and ∧, cf. Section A 3. In particular, these maps commute with ∀K, for any compact K.
Proof Lemma 8.2 and Theorem 9.6. ▫
Corollary 9.12 Closed and compact subobjects coincide in any compact Hausdorff
object, whilst open and overt ones agree in any overt discrete object. ▫


