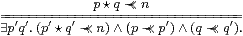



In this section we provide the basic tools for implementing domain theory within ASD. Denotational semantics can then be developed in the usual way using this, allowing programming languages such as Gordon Plotkin’s PCF [Plo77] to be interpreted in ASD, and with them the programs required in Definitions 1.5, 1.6 and 2.3 for computable bases and functions. The difference is that classical domain theory leads to the dead end of set theory, whilst ASD can be translated back into programming languages.
However, the denotational semantics of programming languages will have to wait for a separate investigation. In this section we merely provide a few results that connect ASD with the topological aspects of domain theory such as [JKM99, JKM01, JS96] that rely on manipulation of bases (in the sense of that subject).
We first characterise the objects that have prime bases in our sense, and are continuous dcpos in the classical setting. The following results are essentially those of [Smy77, §2], where ◁ is called an R-structure. However, whereas Michael Smyth imposed a separate theory of recursion on the existing set-based theory of continuous dcpos, recursion is intrinsic to ASD. We also form the domain of rounded ideals using our own technology, which was developed in [B].
Definition 12.1 A directed interpolative relation
n,m:N⊢(n◁ m):Σ on an overt discrete object N
is an open relation that satisfies:
A rounded ideal for (N,◁) is a predicate Γ⊢ξ:ΣN that is
Lemma 12.2 For each n:N, ↓ n ≡ λ k.k◁ n is a rounded ideal. ▫
We shall see that the ↓ n provide the “basic points” pn (cf. Definition 1.5) of continuous and algebraic dcpos. In fact, the situation is summed up by the next result, whose converse we shall prove in Theorem 12.11.
Proposition 12.3
If X has an N-indexed prime basis, so
| φ x ⇔ ∃ n. φ pn ∧ βn x, |
then ≻≻ is a directed interpolative relation, and x:X⊢ξ≡λ n.βn x is a rounded ideal, with
| x = ⋁↑{pn ∣ ξ n}. |
Beware that ≺≺ and ◁ have opposite senses, following the conventions for continuous lattices, cf. the use of ≪ for compact and open subspaces in Notation 1.3: we think of ◁ as relating points. Thus m≻≻ n and m◁ n mean that Am≪ An and pm≪ pn, but βn≪βm.
Proof We have already proved these properties when ≺≺ arises from a filter ∨-basis. An ∨-basis was needed in order to use Scott continuity for An, but in this case An≡λφ.φ pn preserves finite joins too, so directedness is redundant. Briefly,
The directed join is focus(λφ.−) applied to the basis expansion, as in Theorem 10.4. ▫
Examples 12.4 Here again are the prime bases that we have encountered.
| ∃ k.Anβk ⇔ Anβ1 ⇔ An⊤ ⇔ ⊤ Anβr∧ Anβs ⇔ An(βr∧βs) ⇔ An(βr+s). |
Lemma 12.5 Any reflexive transitive relation is directed interpolative,
and then all ideals are rounded. ▫
Examples 12.6
In the classical theory, a domain is recovered from its basis as the (continuous or algebraic) dcpo of (rounded) ideals, with the Scott topology. We can prove the corresponding result within ASD.
Lemma 12.7 For any directed interpolative relation (N,◁),
| Φ:ΣΣN, ξ:ΣN ⊢ E Φξ ≡ ∃ n. Φ(↓ n)∧ξ n |
is a nucleus on ΣN.
Proof We have a directed6 union
| (↓ n) ⇔ λ m.∃ k.(m◁ k◁ n) ⇔ ∃ k.(↓ k) ∧ (k◁ n) |
by the extrapolation and directedness conditions, so by Theorem 9.6 and the definition of E,
| Φ(↓ n) ⇔ ∃ k.Φ(↓ k) ∧ (k◁ n) ⇔ E Φ(↓ n). |
Hence we deduce the equations for a nucleus in Theorem 10.10,
|
Definition 12.8
We have defined E from entirely abstract data
(a directed interpolative relation)
but have shown (via Theorem 10.10)
that it satisfies the characteristic property of the composite
Σi· I that arises from a Σ-split subobject.
Now, it was exactly the purpose of the monadic calculus (Section B 8) that, in this situation, we do have an object, called X≡{ΣN ∣ E} there, that has such a Σ-split inclusion. That is, the calculus provides i:{ΣN ∣ E}↣ΣN and I formally. Then Γ⊢ξ:ΣN is admissible, i.e. an element of the new subobject, if
| Γ, Φ:ΣΣN ⊢ E Φξ ⇔ Φξ. |
The idea of this is that E “normalises” open subobjects Φ of ΣN by restricting and re-expanding them, and it is only the elements of the subobject being defined whose membership of all such Φ remains unchanged in this process.
In this case, the calculus allows us to introduce x≡admitξ:X such that ξ=i x.
Lemma 12.9
ξ:ΣN is admissible iff it is a rounded ideal.
Proof Putting Φ≡λθ.θ n, Φ≡λθ.⊤ and Φ≡λθ.θ r∧θ s, we deduce that ξ is a rounded ideal. Conversely, if ξ is a rounded ideal then
| ∀ m∈ℓ.ξ m ⇔ ∃ k.(∀ m∈ℓ.m◁ k)∧ξ k |
by equational induction on ℓ. Then, using the prime ∧-basis on ΣN,
|
Corollary 12.10 ↓ n is admissible, because it is a rounded ideal. ▫
Theorem 12.11 Any directed interpolative relation
(N,◁) is the opposite of the way-below relation for a prime
basis on its object of rounded ideals.
Proof Let X≡{ΣN ∣ E}↣iΣN in the notation of Section B 8. Now I claim that
| pn ≡ admit(↓ n) and βn ≡ λ x. i x n ≡ Σi(λξ.ξ n) |
define a prime basis. Since ξ≡ i x is admissible, we have the basis expansion,
|
Finally, (n≺≺ m) ⇔ An βm ⇔ βm pn ⇔ i(admit(↓ n)) m ⇔ (↓ n)m ⇔ (m◁ n). ▫
We leave domain theory aside there and return to topology.
Remark 12.12 Jung and Sünderhauf characterise stably locally compact spaces
using a system of rules that they call a strong proximity lattice
[JS96, Section 5].
These axioms are very similar to those in Section 11,
except that theirs are lattice dual, whereas ours are not.
In particular, they prove the dual Wilker property
(Corollary 5.19), albeit using Choice.
If (N,0,1,+,⋆,≺≺) is an abstract basis satisfying
these axioms then so too is (N,1,0,⋆,+,≻≻).
The corresponding object, which is known as the Lawson dual,
classically has the same points as the given one,
but the opposite specialisation order,
whilst the open subobjects of one correspond to
the compact saturated subobjects of the other.
Example 12.13
Let ≺≺ be the way-below relation for a filter lattice basis
on a stably locally compact space X.
The object ℘♯X of rounded ideals for ≻≻
(Example 4)
is called the Smyth or upper powerdomain of X
and is Lawson dual to the topology ΣX. ▫
Lawson duality goes way beyond the purposes of this paper, but we can achieve the dual Wilker property by defining a new basis.
Proposition 12.14 Any stably locally compact object,
i.e. one that has a filter ∧-basis (N,0,1,+,⋆,≺≺),
has another such basis indexed by Fin(N) that also
satisfies the dual Wilker property,
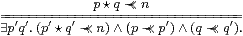
|
This can be extended to a new filter lattice basis with the same property by Lemma 8.4ff.
Proof We define a new version of ⋆, called ×, by
| Ap× q ≡ ∃ p′ q′.Ap′⋆ q′∧(p≺≺ p′)∧(q≺≺ q′). |
This construction, unlike Remark 8.7, preserves the filter property, and is also idempotent.
|
We deduce the dual Wilker property by applying the last equation to βn. Now, as the An preserve ∧,
|
For the converse, we put p‴≡ p′⋆ p″ and q‴≡ q′⋆ q″ and need
| Ap′⋆ q′φ ⇒ Ap′⋆ p″⋆ q′⋆ q″φ and (p≺≺ p′)∧(p≺≺ p″) ⇒ (p≺≺ p′⋆ p″), |
which we have from contravariance of Ap and the fact that we had an ∧-basis. The new operation × can be defined for more factors in the same way, using recursion and equational induction. ▫
General locally compact objects are a good deal more complicated than domains. The extension of the earlier results of this section rely heavily on the “lattice” structure (0,1,+,⋆), which we investigate next.


