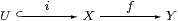



[The best introduction to compact and overt subspaces in ASD is that in Sections J 8 and J 11. See also [G, Section 5].]
The characterisation of open maps in terms of the adjunction ∃f⊣Σf in Section 3 (and of closed maps using Σf⊣∀f in Corollary 5.6) can be generalised to remove the mono requirement.
Unfortunately, as our category need not have all pullbacks, we cannot discuss the Beck–Chevalley condition in the generality that we would like. (We do have it sufficiently often for the purposes of this paper, namely to study the full subcategory of overt discrete objects in Section 10.) For this reason we abstain from giving a generally applicable definition of open map, but, as there is no such problem with Frobenius, we do make the
Definition 7.1
Any map f:Y→ X, not necessarily mono, is called pre-open
if Σf:ΣX→ΣY has a monotone
left adjoint ∃f satisfying the Frobenius law
| ∃f(ψ)∧ φ=∃f(ψ∧ Σfφ) for all φ∈ΣX and ψ∈ΣY, |
where φ and ψ are generalised elements, cf. Remark 2.5 and Proposition 8.2.
The origin of the name open is that (for topological spaces) Σf has a left adjoint satisfying Frobenius iff, for every open subobject i:U↪ X, the image of
is open; indeed the characteristic map of this image is ∃fφ, where φ classifies U. However, this argument does not have any meaning for us, as we do not yet have any notion of direct image, and the one that we shall obtain in Section 10 relies on the present discussion. See [Bou66, §5] for an account of open maps of spaces and [JT84, Chapter V] for the localic version.
Proof [a–c] are obvious. [d] ∃f≡ ∃g · Σe where g≡ f∘ e. [e] Let E≡ Σm·∃g where g≡ m∘ f [the letter E is used to suggest the existential quantifier here, it does not denote a nucleus]. Then we easily have φ⊑Σg·∃gφ=Σf·Σm·∃gφ =Σf· Eφ. Using the hypothesis that Σm is Σ-epi, for the other two properties, it suffices to consider ψ=Σmθ. Then
| E·Σf·Σmθ = E·Σgθ = Σm·∃g·Σgθ ⊑ Σmθ |
and
| E(φ∧Σf·Σmθ) = Σm·∃g(φ∧ Σgθ) = Σm(∃gφ∧θ) = Eφ∧Σmθ. ▫ |
Definition 7.3 Similarly, any map f, not necessarily mono,
for which Σf⊣∀f exists and
satisfies the dual Frobenius law is called pre-proper.
Again, a continuous function between spaces or locales is pre-proper
iff the image of every closed subset of X is closed in Y.
See [Bou66, §§5, 10] for the theory of proper maps of
spaces and [Ver94] for locales,
and the dual Frobenius law in particular.
Closed subsets, proper and pre-proper maps satisfy the analogue of Lemma 7.2.
Remark 7.4 The Beck–Chevalley condition (Propositions 3.11 and 8.1)
is automatic for
(pre-)open
maps of spaces and locales,
but not for pre-proper maps.
In view of the strict duality between them in our theory,
this difference in the traditional ones means that we cannot get
the Beck–Chevalley condition for free in either case.
In keeping with this duality,
it seems inappropriate to employ the usual name closed
for pre-proper maps.
Remark 7.5 André Joyal and Myles Tierney
do construct pullbacks of open maps of locales against arbitrary maps,
and prove the Beck–Chevalley condition
[JT84, Proposition V 4.1].
But they do this with the benefit of
a development of “linear algebra” for sup-lattices,
which are to Abelian groups as frames (locales, as they call them)
are to commutative rings [op.cit., Chapter I].
In particular, the required pullback of spaces is a pushout of frames
and is constructed as a tensor product of sup-lattices,
which is obtained as a coequaliser.
Our categories do not have arbitrary coequalisers,
though it seems plausible that the one that is needed could be constructed
.
Clearly we are currently even less equipped to undertake an analysis
of descent parallel to theirs.
We shall concentrate on the question of whether product projections are open or proper, and on open maps between overt discrete spaces in Section 10.
Remark 7.6 The open–proper symmetry brings us to the question of
why we have three words closed, proper and compact
(not to mention perfect) in one case and only open in the other.
Without them, of course, there would ambiguity over closed but non-compact
subsets of non-compact spaces (Proposition 8.3).
But open sets are equally ambiguous.
[Indeed, we find that overt subspace in real analysis are often also closed,
cf. Definition J 11.1.]
Hence the introduction of the word4 overt for objects, keeping open for the subsets and maps.
Definition 7.7
An object X∈obC is said to be overt
if Σ! has a monotone left adjoint ∃X:ΣX→Σ,
and compact if there is a monotone right adjoint, ∀X.
The Frobenius laws are automatic (Proposition 8.2).
We write ∃ x. φ(x) and ∀ x. φ(x) for ∃X(φ) and ∀X(φ), where φ∈ΣX. Extending the notational convention in Remark 2.5, the range (X) of such a quantifier must be an overt or compact object respectively, whilst the type of the body, φ, like that of a λ-abstraction, must be a power of Σ or the carrier of an algebra.
But there are also other compact predomains, i.e. not necessarily having ⊥. This intriguing possibility is thrown up by our unification of topology and recursion: future work will uncover their significance.
[Since the publication of this paper, Martín Escardó [Esc04] has written extensively on the computational significance of this notion of compactness.]
Remark 7.9 The usual definition of compactness for topological spaces,
that every cover by open subsets has a finite subcover,
can be reformulated in terms of directed joins,
cf. [Joh82, §III 1] for locales.
Our notion of compactness (in the diagram on the right below)
is equivalent to the usual one for LKSp and LKLoc
because ∀X must be a map in the category,
and is therefore Scott-continuous
(Examples 2.11, Remark 7.11).
Proposition 7.10 If the quantifiers and ⊥ exist
then they must form pullbacks as shown.
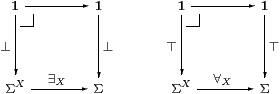
Conversely, if ⊤:1→ΣX is open then its classifier is ∀X.
Likewise, assuming the dual Euclidean principle, if ⊥:1→ΣX is closed then its classifier is ∃X.
Proof ∃Xφ⇔ ⊥ iff φ=λ x.⊥, and ∀Xφ⇔ ⊤ iff φ=λ x.⊤.
Conversely, if {⊤}⊂ΣX is classified by (some map that we call) ∀X then we need to show that ∀X is monotone, id⊑∀X·Σ! and Σ!·∀X⊑id.
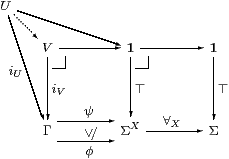
Given φ,ψ∈ΣX with φ⊑ψ, let U,V⊂Γ be their pullbacks against ⊤:1→ΣX, which exist because ∀Xφ and ∀Xψ classify them. Then ψ∘ iU⊒φ∘ iU=⊤, whence U⊂ V, so ∀Xφ⊑∀Xψ by uniqueness of classifiers.
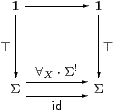
Both of these squares commute, but the one with id is a pullback, so comparing the other with the pullback that it contains we have
| 1≡ [id]⊂[∀X·Σ!], |
and so the required inequality follows by uniqueness of classifiers.
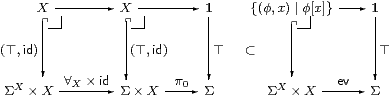
The two lower composites are the exponential transposes of Σ!·∀X and id respectively, and both diagrams are pullbacks. So to obtain the required inequality (again using uniqueness of classifiers) we only need to check that one subset is contained in the other, but clearly φ[x]=⊤ when φ=λ x.⊤. (We have equality when X is inhabited, but not when it’s empty.)
The analogous result for ∃X depends on the dual Euclidean principle, since we rely on uniqueness of classifiers using ⊥. ▫
Remark 7.11
The simplest way of imposing Scott-continuity is the equation
| F(λ x:ℕ.⊤) ⇔ ∃ n:ℕ.F(λ x:ℕ.x< n) for all F∈ΣΣℕ |
which was called the Scott Principle in [Tay91]. In this situation, ℕ cannot be compact, because F=∀ℕ would satisfy
| ∀ℕ(λ x.⊤)≡(∀ x:ℕ.⊤)⇔⊤ ∀ℕ(λ x.x< n)≡(∀ x:ℕ.x< n)⇔⊥, |
making the two sides of the Scott principle ⊤ and (∃ n.⊥)⇔⊥. ▫
Whilst Scott continuity pervades the motivations of Abstract Stone Duality, it is remarkable how many theorems we can prove before we need to invoke it as an axiom. In particular, the search or minimalisation operator µ:(2⊥)ℕ→ℕ⊥ for general recursion can be constructed without using it [D], but we do need it for the function-space (ℕ⊥)ℕ [F]. For all of the investigations that I have done so far in general topology, the Phoa principle and monadicity have been enough.
Proposition 7.12 If X is overt and discrete
(in particular X≡ ℕ) then
{ }X:X↣ΣX is a Σ-split mono,
i.e. there is a map I:ΣX↣ΣΣX such that
Σ{ }X· I=idΣX.
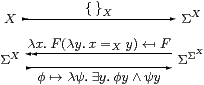
This subspace is in general neither open nor closed, but
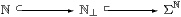
assuming the Scott principle [D, F]. ▫


