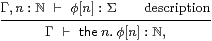



We have seen that focus is redundant for types of the form ΣX, since they are all sober, so ℕ is the only type of the restricted λ-calculus that still needs to be considered. In fact, if it is defined to admit primitive recursion alone, as in Remark 2.5, it has points “missing”. These may be added in various equivalent ways, using
Remark 9.1
The relevant property of ℕ in the first part of the discussion
is not recursion, but the fact that there are morphisms
| ∃ℕ:Σℕ→Σ and (=ℕ):ℕ×ℕ→Σ |
with the expected logical properties. Objects that carry these structures are called overt and discrete respectively Sections 6–8.
The whole of this paper (apart from Section 5) also applies to the category of sets and functions, or to any topos. There ΣX is the powerset, more usually written ΩX, and ηX(x) is the ultrafilter of subsets to which x∈ X belongs. All sets are overt and discrete, so the argument that follows (up to Corollary 10.5) applies to them as well as to the natural numbers. See [LS86, Section II 5] for a discussion of definition by description in a topos, the crux of which is that {}:X→ΣX is a regular mono, cf. our Definition 4.7 for sobriety.
Lemma 9.2 [a/x]*φ ⇔ ∃ n.φ[n]∧(n=a),
cf. Lemma 8.7. ▫
Definition 9.3
A predicate Γ, n:ℕ⊢φ[n] is called a description
if it is uniquely satisfied, i.e.
| Γ ⊢ (∃ n.φ[n]) ⇔ ⊤ and Γ, n,m:ℕ ⊢ (φ[n]∧φ[m]) ⇔ (φ[n]∧ n=m). |
We shall refer to these two conditions as existence and uniqueness respectively. Using inequality, uniqueness may be expressed as
| Γ ⊢ (∃ m,n.φ[m]∧φ[n]∧ n≠ m) ⇔ ⊥. |
Definition 9.4 Any description entitles us to introduce its numerical witness,
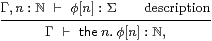
|
the elimination rule being the singleton
| n:ℕ ⊢ |
| ≡ (λ m.m=n) :Σℕ, |
which is easily shown to be a description. Then the β- and η-rules are
| Γ, n:ℕ ⊢ (n=the m.φ[m]) ⇔ φ[n] and n:ℕ ⊢ (the m.m=n) = n. |
The restricted λ-calculus, together with the lattice structure and primitive recursion in Remarks 2.4–2.5 and these rules, is called the description calculus.
Lemma 9.5
Let Γ, n:ℕ ⊢ ψ[n]:Σ be another predicate.
Then, assuming these rules,
Proof By Lemma 9.2, ψ(the n.φ[n]) ⇔ ∃ m.ψ[m]∧(m=the n.φ[n]), which is ∃ m.ψ[m]∧φ[m] by the β-rule for descriptions. ▫
[The statement and proof of the following result were incorrect in the published version of this paper; this version appeared as Lemma E 2.8. It turns recursion at type ℕ into recursion at type Σℕ, as part of the process of bringing descriptions (the m.) to the outside of a term.]
Lemma 9.6 Γ ⊢ r n ≡
rec(n, z, λ n′ u. s(n′,u)) = the m.ρ(n,m) , where
|
Proof The base case (in context Γ) is
|
The induction step, with the hypothesis λ m′.ρ (n, m′) = λ m′.(m=r n′), is
|
So Γ, n:ℕ ⊢ λ m.ρ(n,m) = λ m.(m=r n). ▫
Hence we have the analogue of Proposition 8.10 for descriptions.
Proposition 9.7
Any term Γ⊢ a:X in the description calculus is provably equal
Proof By structural recursion on the term a, in which Lemmas 9.2, 9.5 and 9.6 handle the non-trivial cases. ▫
Remark 9.8 As in Remark 8.3 for focus,
we must be careful about the scope of the description,
— how much of the surrounding expression is taken as the formula ψ?
For F:ΣΣ, does
| F(ψ(the n.φ[n])) reduce to F(∃ n.φ[n]∧ψ[n]) or to ∃ n.φ[n]∧ F(ψ[n]) ? |
Once again, it does not matter, as they are equal, so long as φ is a description. Otherwise, they are different if F(⊥) ⇔ ⊤, for example if F≡λσ.⊤ or (in set theory) F≡¬.
Remark 9.9 The theory of descriptions was considered by Bertrand Russell
[RW13, Introduction, Chapter III(1)]
[vH67, pp 216–223]
[GG00, Section 7.8.4].
The theme of his development is that the n.φ[n] is incomplete:
it acquires a meaning only when embedded in a predicate ψ,
as in Lemma 9.5.
(This came out of his dispute with Hugh McColl and Alexius Meinong
regarding grammatically correct noun-phrases that don’t denote
[GG00, Section 7.3].)
Russell defined
| ψ[the n.φ[n]] as ∃ n. ψ[n]∧φ[n]∧(∀ m.φ[m]⇒ n=m), |
incorporating the condition of unique satisfaction as a conjunct in this predicate. He used an inverted iota for the description operator.
So long as φ is a description, Russell’s definition is equivalent to our β-rule, but ∀ is not a symbol of our calculus — for the reasons that we set out in Section 1.
Gottlob Frege had treated the description operator as an everywhere-defined function-symbol, written \ [Fre93, §11] [GG00, Section 4.5.6]. He therefore had to make a case-distinction, in which \φ returns the member of a singleton class, but the class itself if it is not a singleton. A 1960s logic textbook that I prefer not to advertise assigns [the value] 0 [to any expression] the n.φ[n] whenever φ fails either of the conditions for being a description, with the result that
is true since 0=0 (and this book had two authors).
As we have observed, if we are allowed to write the n.φ[n] without φ satisfying the condition, then all sorts of mathematical transformations that we would normally expect to be able to make become invalid. Frege’s case-distinction is not computable — we have first to determine the cardinality of the class, which may involve answering an arbitrarily difficult mathematical question. It also illustrates the untyped nature of his calculus (which was a part of its downfall): if we introduce a=the x.φ[x], we at least expect φ[a] to be meaningful (though maybe false if φ is unwitnessed), which it is not if a is a set. Even Russell’s good intentions of enforcing the description property are frustrated by his object-language implementation, as it may result in some larger formula becoming true contrary to common sense.
Giuseppe Peano [Pea97] [GG00, Section 5.4.3] had also recognised the incomplete nature of description-phrases in mathematics. On the other hand, he required the predicate to be a description as a premise to the definition of the operator, for which he wrote ι, using ι a for our {a}. So, the condition of unique satisfaction is part of the meaning in a meta-logical way: if the author has written the n.φ[n] anywhere, there is an implicit claim that φ has been proved to be a description, and this fact may be re-used anywhere in the argument. This is the point of view that we have taken: it is a side-condition on the well-formedness of the expression. At the very least, it documents the fact, and to rely on some exceptional behaviour is hacking.
Whilst Russell’s extension of Peano’s iota to non-descriptions is questionable, from our denotational point of view, he did take the technical analysis a step further by considering the scope of the expression, as in Remark 9.8.
[Claus-Peter Wirth felt that I have done a dis-service to Peano here, and drew my attention to [Pea97, §22]. In my own translation of the text and the notation, this reads
..., let α be a class containing a single member, that is:We call this member ια. That is
- there is an α, and
- whenever we take two things x and y from α, these must always be equal.
This definition really gives a meaning to the whole formula x=ια, and not just to the combination ια.
(∃ x.x∈ α), (∀ x y.x, y∈ α⇒ x=y) ⊢ (x=ια) ⇔ (α=
⎧
⎨
⎩x ⎫
⎬
⎭). Any proposition containing ια is reducible to the form ια∈φ, where φ is a class, and hence to α⇒φ, from which the sign ι has disappeared, even though we can’t form an equality whose first member is ια and the second is a group of known symbols [i.e. define ια in terms of known symbols].
This contains at least a hint of Proposition 9.7, long before other people had the syntactic or proof-theoretic tools to prove normalisation theorems.]
The obvious way to find the n.φ[n] is to search for the least n that satisfies φ[n]. In order to be sure that it is the least, we must check ¬φ[m] for each m< n along the way.
Definition 9.10 Γ⊢α:Σ is said to be
complemented or decidable if there is some (unique)
Γ⊢β:Σ such that α∧β⇔⊥ and
α∨β⇔⊤. We write ¬α for β.
| Γ, n:ℕ ⊢ φ[n] ≡ ψ[n]∧∀ m< n.¬ψ[n] |
Remark 9.12
The search operator µ is usually defined without the existence and
decidability conditions (ψ being replaced by a partial function
ψ:ℕ⇀2), and then itself defines a partial function,
i.e. a program that need not terminate.
The universal property of ℕ, as formulated in category theory by Bill Lawvere, is known in logic as primitive recursion. Adding the search operation gives general recursion. This is known to be properly more powerful, as functions can be defined using it that grow much faster than is possible using primitive recursion alone. Since, as we show in the next section, definition by description in ℕ is equivalent to sobriety, the way that we described in Section 1 of defining computational values via observations really does define bigger numbers than we could obtain directly. (At any rate, it defines bigger functions, but since functional notation such as 10n and its generalisations are essential for writing big numbers, it is widely argued that general recursion does indeed define bigger numbers.)
Although general recursive functions are partial, we would prefer to treat them as total functions ℕ→ℕ⊥ into the lift. This object may be seen as a closed subspace of Σℕ, but its construction in abstract Stone duality makes rather serious use of the lattice structure on Σ [D][F].
Remark 9.13
When we add subspaces to our calculus in [B],
we find that a predicate that is a description on the subspace of interest
may no longer satisfy the existence and uniqueness criteria
on the ambient space.
Conversely, any predicate becomes a description when restricted to
the (possibly empty) locally closed subspace
defined by the ⊤ and ⊥ equations in Definition 9.3.
Nevertheless, it turns out that the n.φ[n] may be manipulated
on the subspace by using the β-rule as we have given it,
but on the ambient space,
even though this it is not a well formed expression there.
Although the reduction may result in expressions with different meanings
on the ambient space, they agree as intended on the subspace.


