


We now give a new characterisation of dominances in terms of the object Σ (and its powers) alone, without any reference to subsets. These are supplied by the monadic assumption, which therefore somehow plays the role of the axiom of comprehension. [This role is formalised in Section B 8.]
Proposition 3.1
In any dominance Σ, the Euclidean principle
| φ(x) ∧ F(x,φ(x)) ⇔ φ(x) ∧ F(x,⊤) |
holds for all φ:X→Σ and F:X×Σ→Σ.

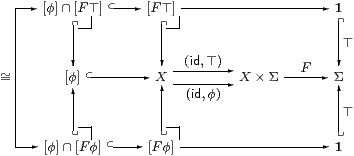
Proof The composites [φ]↪ X⇉ X×Σ→Σ are equal by the construction of [φ]↪ X, so their pullbacks [φ]∩[F⊤] and [φ]∩[F φ] along ⊤ are isomorphic, i.e. equal as subobjects of [φ], and so of X. Since [ ]:C(X,Σ)→SubM(X) preserves ∩, these subobjects are [φ∧ F⊤] and [φ∧ F φ] respectively. But then, by the uniqueness of the characteristic map, the equation holds. ▫
Another construction that we can do with a dominance will turn out to be the existential quantifier. [For this reason the letter E was used for it in the published version of this section, but this has been changed to I here because of the convention that was adopted later in the ASD programme of using E for a nucleus.]
Lemma 3.2
Using Definition 2.2,
let i:U↪ X be the mono classified by φ:X→Σ.
Then the idempotent (−)∧ φ on ΣX splits into
a homomorphism Σi and another map I:ΣU↣ΣX
with Σi· I=idΣU
and I·Σi=(−)∧φ:ΣX→ΣX.
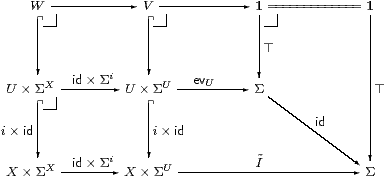
Proof Let V and W be the middle and left pullbacks in the top row, and let Ĩ be the classifying map for V↪ X×ΣU, so the big square is also a pullback.
Now consider how V↪ U×ΣU is classified by maps targeted at the lower right corner. One classifier is id∘evU. However, whilst V was defined as the pullback of Ĩ against ⊤, it is also the pullback of the composite Ĩ∘(i×id) against ⊤, where the relevant triangle commutes because i×id is mono. Hence Ĩ∘(i×id) also classifies V. By uniqueness, the trapezium commutes, and the exponential transposes are Σi· I=id.
The composite along the bottom is the transpose of I·Σi. The lower left square is a pullback, so the whole diagram is a pullback and W is {(x,ψ)∈ X×ΣX ∣ I(Σiψ)(x)}. However, using the smaller pullback rectangle, it is {(x,ψ) ∣ x∈ U∧ ψ(x)}, where (x∈ U) means φ(x). Again by uniqueness of (pullbacks and) the classifier, these are equal, so I·Σi=(−)∧φ. ▫
The significance of the Euclidean principle and the map I is that they provide an example of the condition in the theorem of Jon Beck that characterises up to equivalence the adjunction between the free algebra and underlying set functors for the category of algebras of a monad [Mac71, §IV 7] [BW85, §3.3] [Tay99, §7.5]. Although the public objective of the theory of monads is as a way of handling infinitary algebra, this condition will turn out to be more important in Abstract Stone Duality than the notion of algebra.
Lemma 3.3
Let Σ be an exponentiating semilattice that satisfies the
Euclidean principle (i.e. the conclusion of Proposition 3.1).
Then the parallel pair (u,v) in the middle of that diagram,
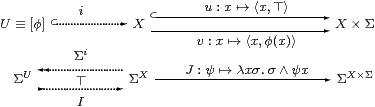
is Σ-split in the sense that there is a map J as shown such that
| (Jψ)(u x)⇔ψ(x) and J(F∘ u)(v x)⇔ J(F∘ v)(v x) |
for all x∈ X, ψ∈ΣX and F∈ΣX×Σ. (We just mark u with a hook as a reminder that these equations are not symmetrical in u and v.)
Proof For ψ∈ΣX, we have (Jψ)(u x)⇔ ⊤∧ψ(x)⇔ ψ(x) and (Jψ)(v x)⇔ φ(x)∧ ψ(x). Hence J(F∘ u)(v x)⇔ φ(x)∧ F(x,⊤) and J(F∘ v)(v x)⇔ φ(x)∧ F(x,φ(x)), which are equal by the Euclidean principle. ▫
Remark 3.4 The map I defined in Lemma 3.2
is the fifth one needed (together with Σu and Σv) to make
the lower diagram in Lemma 3.3 a split coequaliser.
| idΣU=Σi· I I·Σi=(−)∧φ=Σv· J. |
[The term E≡ I·Σi≡λψ.ψ∧φ is a nucleus (Definition B 4.3 and §O 8.3):
|
using the Euclidean principle with σ≡φ x. Then
| U≡{X ∣ E} and x∈ U⊣⊢φ x⇔⊤⊣⊢∀ψ. Eψ x⇔ψ x |
in the notation of Section B 8.] ▫
Remark 3.5
Since Σ is a semilattice, it carries an internal order relation.
Some morphisms are monotone with respect to this order,
but others may not be.
The order also extends pointwise to an order on morphisms
between (retracts of) powers of Σ.
We shall discuss monotonicity,
and some other ways of defining order relations, in Section 5.
The order also allows us to talk of such morphisms as being adjoint, L⊣ R.
When the definition of adjunction is formulated as the solution of a universal property, the adjoint is automatically a functor. However, the definition that is most useful to us is the one that uses the internal order relation and the structure of the category directly, namely
| id⊑ R· L L· R⊑id, |
which does not itself force L and R to be monotone. So we say so, even though we have no intention of considering non-monotone adjunctions. This point is significant in Lemma 3.7 in particular. To repeat Proposition 2.8,
Lemma 3.6 For any object Z, the functor (−)Z
(defined on the full subcategory of retracts of powers of
an exponentiating semilattice Σ)
preserves the semilattice structure,
and hence the order (i.e. it is monotone or order-enriched)
and adjointness (LZ⊣ RZ). ▫
Lemma 3.7
Let P:A→ S be a homomorphism between internal semilattices
and I:S→ A another morphism such that idS=P· I.
Then the following are equivalent:
| I(θ)∧ψ = I(θ∧ Pψ) for all θ∈ S, ψ∈ A; |
In this case, I preserves binary ∧, so it is monotone, and I⊣ P. Since the [order relation ⊑ derived from a semilattice structure is] antisymmetric [i.e. φ⊑ψ, ψ⊑φ ⊢ φ=ψ], adjoints are unique, so each of P, I and φ uniquely determines the other two. (See Definition 10.4 for when I preserves ⊤.)
Proof [a⇒b] I(θ)∧ ψ = I· P· I(θ)∧ ψ = (Iθ∧φ)∧ ψ, whilst
| I(θ∧ Pψ) = I(P· I(θ)∧ Pψ) = I· P(I(θ)∧ψ) = (Iθ∧ψ)∧ φ |
since P preserves ∧.
[a⇐b] I· P(ψ) = I(⊤∧ Pψ) = I(⊤) ∧ ψ, so φ=I(⊤).
In particular, I(θ1)∧ I(θ2) = I(θ1∧ P· I(θ2)) = I(θ1∧θ2). Finally, I⊣ P because idS⊑ P· I and I· P⊑idA. ▫
Now we apply the monadic property to logic for the first time.
Remark 3.8 Instead of taking the class M of monos as fundamental,
from now on we shall assume that
Lemma 3.9
With the assumptions in Remark 3.8,
let φ:X→Σ in C. Then
So we have a class M of monos with an exponentiating classifier Σ, as in Section 2.
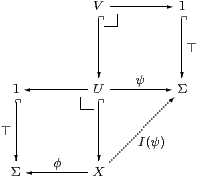
Proof The pullback is given by an equaliser; Lemma 3.3 shows that this pair is Σ-split, using the Euclidean principle, so the equaliser exists by Beck’s theorem, and the contravariant functor Σ(−) takes it to the (split) coequaliser. Thus the idempotent (−)∧ φ on ΣX splits into a homomorphism Σi:ΣX↠ΣU and a map I, satisfying the equations above. By Lemma 3.7, I⊣Σi and the characteristic map φ≡ I(⊤) is unique. Finally, if V is classified by ψ:U→Σ then the composite i∘ j is classified by I(ψ). [See §O 8.4 for a more detailed proof of (d).] ▫
Theorem 3.10
Let (C,Σ) satisfy the first four axioms in Remark 3.8. Then
In this case, a mono i is classified (open) iff there is some map I that satisfies id=Σi· I and the Frobenius law.
Proof [More explanation of how the Euclidean principle entails uniqueness of classifiers is needed. This is trivial in the case of ⊤ since the square
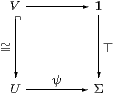
is only a pullback (indeed, commutes) when ψ=⊤. More generally, if φ,ψ:X⇉Σ have the same pullback U then so does φ∧ψ (cf. Proposition 2.8), so without loss of generality ψ⊑φ. Using the foregoing argument, this situation transfers from X to U. The role of the Euclidean principle, or more precisely the Frobenius law, is to make ΣU≅ΣX↓φ (Lemma 3.7). The external form of this relationship is the top row of the diagram
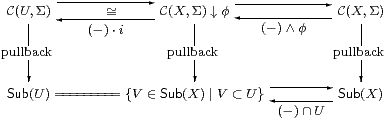
in which the bottom row says the same thing for (open) subspaces, using the fact that open inclusions compose (Lemma 3.9(d)). We also know that the diagram commutes in the obvious ways. Hence if ψ⊑φ:X⇉Σ both classify U then ψ factors through U→Σ and as such it classifies the same open subspace of U as ⊤ does, namely U itself, so ψ=⊤:U⇉Σ, Since C(U,Σ)≅C(X,Σ)↓φ we have ψ=φ:X⇉Σ.] ▫
This result partly answers a criticism of [Tay91], that it did not ask for a dominance, since the Euclidean principle is a part of the Phoa principle (Proposition 5.7), although monadicity was not considered there.
It does not seem to be possible, in general, to deduce id=Σi· I from the simpler condition that i be mono (with I⊣Σi), but see Corollary 10.3 when the objects are overt and discrete.
The next result justifies the name ∃i for I [Tay99, §9.3], although it only allows quantification along an open inclusion: we consider the more usual quantifier ranging over a type in Sections 7–8.
Proposition 3.11
For i:U↪ X open, Σi and ∃i satisfy
| ∃i(θ)∧ ψ = ∃i(θ∧Σiψ) |
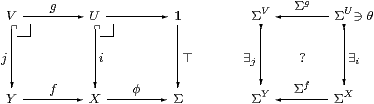
for any map f:Y→ X in C, i.e. that if the square consisting of g, i, f and j is a pullback then that on the right commutes.
Proof [a] Lemma 3.7. [b] Put ω≡ ∃i(θ), so θ=Σi(ω) and ω=∃iΣi ω=ω∧ φ. Then ∃jΣg θ = ∃j Σg Σi ω = ∃j Σj (Σf ω) = Σfω∧ (φ∘ f) = Σf(ω∧ φ) = Σfω = Σf∃iθ since φ∘ f classifies j:V↪ Y. ▫
Remark 3.12
Consider the pullback (intersection) U∩ V⊂ X of two open subsets.

In the diagram on the right, the monos are existential quantifiers and the epis are inverse images, which are adjoint and split. The Beck–Chevalley condition for this pullback says that the squares from ΣU to ΣV and vice versa commute. These equations make the square of existential quantifiers an absolute pullback, i.e. it remains a pullback when any functor is applied to it, and similarly the square of inverse image maps an absolute pushout [Tay99, Exercise 5.3]. ▫
Remark 3.13 The Euclidean equation can be resolved into inequalities
| σ∧ F(ψ)=⇒ F(σ∧ψ) σ∧ F(σ∧ψ)=⇒ F(ψ) |
for all σ∈Σ, F:ΣY→ΣX and ψ∈ΣY. The first says that F is strong, and the second is a similar property for order-reversing functions. At the categorical level, the contravariant functor Σ(−) also has such a co-strength, X×ΣX× Y→ΣY, given by (x,ω)↦λ y.ω(x,y). ▫


