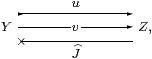



The rest of the paper shows (in three different ways) how to construct a category S in which we may form subspaces as just described, i.e. equalisers of Σ-split pairs that Σ(−) takes to coequalisers. As raw material, we simply require a category S with finite products and an exponentiating object Σ, such that all objects of S are sober. A category S of this kind was defined using a λ-calculus in Section A 8. In Section 7 we shall see that Algop does the job, but first we do it by adding formal equalisers of Σ-split pairs.
This construction is similar to that of the so-called Karoubi completion of a category, which forces it to have splittings of idempotents. However, as the new construction is rather more complicated, you would be well advised to (re)familiarise yourself with the simpler version by proving
Remark 4.1
The Karoubi completion, KS, of any category S has
Then
[The use of the letter K is unfortunate, as it conflicts with Kuratowski-finiteness in [E].]
From a categorical point of view, it would be easier to assume that idempotents split in S. This would “modularise” the construction of S as S↦KS↦AlgKS↦S. However, our intention (in Section 10) is to reduce computation in S back to the restricted λ-calculus, i.e. S. KS already has some subspaces for the convenience of mathematicians, whereas the idempotents infest computations in it, so it has already crossed the line of demarcation between these subjects. For this reason, we develop a representation of S-objects directly in terms of S that splits idempotents as well as equalisers.
Definition 4.2
A typical object X of our category S is a Σ-split pair
(Definition 3.7),
which we may write using Notation 2.11 simply as
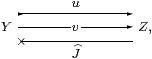
such that u;J=idY and v;J;u=v;J;v:Y−× Z. This object will temporarily be called (Y⇉ Z), or just X, in parts of the argument up to Section 6.
The identity morphism on this object will be E ≡ v;J. As in the Karoubi construction, this is an idempotent endomorphism of Y, but in the auxiliary category HS. In fact, its defining equation is stronger than idempotence.
Definition 4.3 E:ΣY→ΣY
is called a nucleus on Y if
E;ηY;ΣE=E;ηY, or
| F:Σ3 Y ⊢ E(λ y.F(λφ.Eφ y)) = E(λ y.F(λφ.φ y)) |
using the λ-calculus. Observe carefully that the left hand side has an extra E.
We shall write {Y ∣ E} instead of (Y⇉ Z) for an object of S defined in terms of E like this.
When E is a first class map (E ≡ Σe and e ≡ E), the equation is just idempotence (e=e;e). In general, however, it says more than E=E;E, for the same reason that we remarked in Definition 2.3, namely that, in the splitting of this second class idempotent as I;i, the inclusion part i must actually be first class.
Notation 4.4
Given two nuclei, E1 and E2,
we write E2⊂YE1 if
| ; |
| = |
| = |
| ; |
| . |
Definition 4.5
A typical morphism from {Y1 ∣ E1} to {Y2 ∣ E2}
is an HS-map H:Y1−× Y2 such that
| = |
| ; |
| and |
| ;ηY1;ΣH = |
| ;ηY2, |
the first equation being equivalent to H;u2=H;v2 when {Y2 ∣ E2} is defined by the pair u2,v2:Y2⇉ Z2. Using λ-calculus, the second equation is
| G:Σ3Y2 ⊢ E1(λ x:Y1.G(λψ:ΣY2.Hψ x)) = H(λ y:Y2.G(λψ.ψ y)), |
which adds E1 to the λ-equation for a homomorphism (Remark A 4.11).
Lemma 4.6
Any morphism
H:{Y1 ∣ E1}→{Y2 ∣ E2}
also satisfies H=E1;H.
Proof
|
▫
Lemma 4.7 For any split pair, E ≡ J;Σv is a nucleus
(Definition 4.3); in particular, E is idempotent in HS.
Proof The equation for E is the same as the second one for a morphism H ≡ E in Remark 4.5. It follows from the defining equations for u, v and J:
|
The first equation for a morphism is idempotence of H ≡ E, which follows from the previous result, but explicitly from the u v J equations,
| ; |
| = v; |
| ;v; |
| = v; |
| ;u; |
| = v; |
| = |
| . ▫ |
Proposition 4.8
S is a category.
Proof We have to show that composition is well defined. Let H:Y1→ Y2 and K:Y2→ Y3. Then H;K;E3=H;K=K;H and
|
so H;K satisfies the definition of a morphism. Associativity is inherited from S, whilst the equations that say that E is the identity on {Y ∣ E} are those in Definition 4.5 and Lemma 4.6. ▫
Remark 4.9 Although there is more to the data for an object of S
than the maps u and v,
the justification of calling such an object a “pair”
is that, if we have two splittings J1 and J2,
then E1≡ v;J1 and E2≡ v;J2
define an isomorphism between these objects of S.
For example, we shall see in Proposition 5.12 that the binary product
of any two non-trivial objects has two different splittings.
Lemma 4.10
S is embedded as a full subcategory of S by
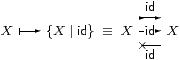
| f:X→ Y ↦ H≡Σf:ΣY→ΣX. |
(Recall that we assume that all objects of S are sober.) ▫
Remark 4.11
Definition 2.10 provided another embedding,
which represents X by its standard resolution,
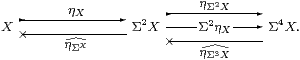
This makes
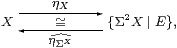
where E ≡ ηΣ3 X;Σ3ηX = ΣηX;ηΣX by F↦λ F.F(λ x.F(λφ.φ x)). ▫
The nucleus E is enough on its own to represent the object.
Lemma 4.12
For any object (Y⇉ Z), we have the isomorphism in S
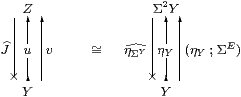
encoded by E ≡ v;J in both directions.
Proof The object on the right gives rise to the same nucleus because
| ηY;ΣE; |
| = ηY; |
| ; |
| = |
|
by naturality and the unit law. It satisfies Definition 4.2 because ηY;ηΣY=idY and
| ;ηY;ΣE = |
| ;ηY |
since E is a nucleus. Hence both objects are {Y ∣ E}, on which E is the identity, and it also serves as the isomorphism in both directions. ▫
Proof Given
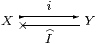
with i;I=idX, put E=I;i as in Remark 2.9.
This satisfies the E equation because
| ;i;ηY;ΣI;Σ2 i = |
| ;ηX;Σ2 i;ΣI;Σ2 i = |
| ;ηX;Σ2 i = |
| ;i;ηY |
by naturality of η and i;I=idX. For composition, E≡ i1;i2;I2;I1. ▫
Although E suffices to describe an object of the new category, and will be used in the new calculus in Section 8, it is not very illuminating. The reason for introducing the Σ-split pair (Y⇉ Z) is that the new object is its formal equaliser, as in Proposition 3.8.
Proposition 4.14
Every object (Y⇉ Z) of S
is the equaliser in S of the diagram that it suggests,
considered to consist of images (via Lemma 4.10)
of objects and maps in S.
If this diagram already has an equaliser X in S,
and Σ(−) takes it to a coequaliser in S,
then (Y⇉ Z)≅ X in S.
Proof For any object Γ ≡ (Y0⇉ Z0) of S, we check that an HS-map H:Y0−× Y satisfies the conditions for being a S-map Γ→(Y⇉ Z) iff it satisfies those for being a S-map Γ→(Y⇉ Y) that has equal composites with u and v. This is simply a matter of changing the status of the equation H;u=H;v from being part of Definition 4.5 of a S-morphism to being a test for the equaliser.
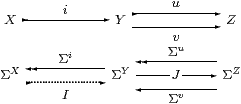
For the second part, J;Σv:ΣY→ΣY has equal composites with Σu and Σv, whose coequaliser is ΣX by hypothesis, so E ≡ J;Σv=Σi;I for some I as shown. Both I;Σi and id mediate from the equaliser to ΣX, so are equal by uniqueness. Then i:X→(Y⇉ Z) is an isomorphism, with inverse I:(Y⇉ Z)→ X. ▫
As the construction of S is one that “freely adjoins equalisers” we would expect at this point to have to show that S does in fact have such equalisers, including those for newly defined parallel pairs, and that Σ(−) takes them to coequalisers. However, in our case, powers of Σ are involved in this statement, whereas we still have a lot of work to do to construct such powers in S. This will be done in Proposition 6.10.
We draw one easy corollary from the Proposition here, largely to show the contrast with the more difficult study of products that follows in the next section.
Proposition 4.15
The functor S→S preserves such colimits as exist.
Proof Let (Ui) be a diagram in S. Any cocone under it with vertex (Y⇉ Z) in S is, by the previous result, a cocone with vertex Y such that for each i the composites Ui→ Y⇉ Z are equal. But this cocone might as well be in S , and has a mediator U ≡ colim Ui→ Y, which also has equal composites U→ Y⇉ Z, and is therefore a mediator U→(Y⇉ Z) in S. ▫


