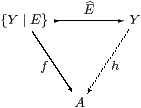



We know from Section A 6, and from the work on continuations by others cited there, that binary products are the crucial issue. These studies have also taught us that we must take just one step at a time. In Section 7 below we sketch the construction of products in S as coproducts of algebras, but the motivation of that approach involves the anticipation of results that ought to follow from the conclusion itself.
In this section we argue forwards from the structure in the given category S, using basic (albeit pedestrian) categorical ideas, and sticking to the objects rather than their algebras of predicates. The plan is to regard S-objects as equalisers in S as in Proposition 4.14, and then use the given products in S.
However, the universal property of these given products is only tested by diagrams of the form Γ→ A× B with Γ∈obS, so we need to generalise this to Γ∈obS. This is more difficult than the situation for colimits in Proposition 4.15: in this case we need to be able to turn maps {Y ∣ E}→ A into Y→ A, which is just the property of injectivity from which we began in Remark 2.1.
Definition 5.1 An object A of S is said to be injective if,
for any subspace inclusion {Y ∣ E}↣ Y
and map f:{Y ∣ E}→ A, there is some (not necessarily unique)
map h:Y→ A such that f=E;h.
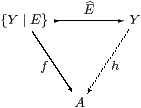
Proposition 5.2
An object A of S is injective iff it is a retract of some ΣU
(by which we still mean the exponential in S).
Indeed, when A∈obS is injective, there is a map α:Σ2 A→ A
such that ηA;α=id, though this need not satisfy the
other equation that is required for (A,α) to be
an Eilenberg–Moore algebra, namely µA;α=Σ2α;α.
Proof (⇐) Suppose first that A ≡ ΣU, and put α ≡ ΣηU. By Definition 4.5, any morphism H:{Y ∣ E}→ A in S satisfies
| = |
| ;ηA;α = |
| ;ηY;ΣH;α = |
| ;h, |
where h ≡ ηY;ΣH;α is in S. The result extends to retracts of ΣU by composition with the inclusion and surjection.
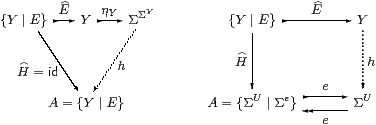
(⇒) The composite {Y ∣ E}↣Σ2 Y is a subspace by Corollary 4.13; injectivity says that this is split by h. When A ≡ Y∈obS, α ≡ h satisfies ηA;α=id. ▫
Corollary 5.3
S has enough injectives:
each object {Y ∣ E} is a subspace of some injective Σ2 Y. ▫
Examples 5.4 In LKSp, the injectives are the continuous lattices equipped
with the Scott topology [Sco72a],
whilst the algebras are also distributive.
In Set, injectives are (sets that carry the structure of) complete lattices,
and algebras are powersets
(which, classically, are complete atomic Boolean algebras). ▫
Lemma 5.5
Any finite product of injectives (or algebras)
is again injective (respectively, an algebra).
Proof For the terminal object, α ≡ !ΣΣ.
For injectives (A,α) and (B,β), we define P0 ≡ Σ2π0;α:Σ2(A× B)→ A and P1 ≡ Σ2π1;β :Σ2(A× B)→ B, and then ηA× B;<P0,P1>=id. This follows from naturality of η, as illustrated in the right-hand trapezium below.
Moreover, if (A,α) and (B,β) are algebras then
|
so (A× B,<P0,P1>) is also an algebra. ▫
Lemma 5.6 The functor S→S preserves the terminal object.
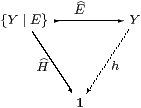
Proof Since 1 is injective, E;!Y is the only map H:{Y ∣ E}→1. ▫
Lemma 5.7
The functor S→S preserves binary products
of injectives.
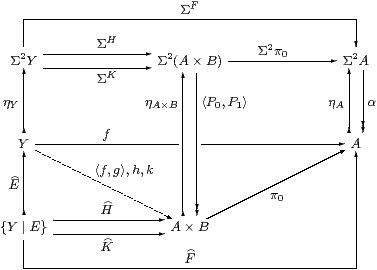
Proof Let F:{Y ∣ E}→ A and G:{Y ∣ E}→ B in S. Put
| f ≡ ηY;ΣF;α and g ≡ ηY;ΣG;β, |
so F=E;f and G=E;g by Proposition 5.2, and <f,g> is given by the product in S.
Then H≡E;<f,g>:{Y ∣ E}→ A× B satisfies H;π0=F and H;π1=G.
Suppose that H and K both satisfy these equations. Using Lemma 5.5, put
| h ≡ ηY;ΣH;<P0,P1> and k ≡ ηY;ΣK;<P0,P1>, |
so H=E;h and K=E;k by Proposition 5.2.
Since ΣH;Σ2π0=ΣF=ΣK;Σ2π0, we have h;π0=f=k;π0 by the way in which h, k and f were constructed, and similarly h;π1=g=k;π1. Hence h=k=<f,g>, as these maps are in S, so H=K. ▫
Now we can begin the main business of this section. In view of Corollary 5.3, we may assume that the S-objects of which we want to form the product are given by Σ-split pairs of maps between injectives. In fact this restriction will become redundant, as the argument below can be used first to show that all products are preserved, and then to construct products of non-injective pairs.
Lemma 5.8
Let (Y⇉ Z)∈obS and W∈obS.
Then
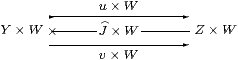
is also an object of S. It is called (Y⇉ Z)× W because, at least when U, V and W are injective, this is the product in S. In the comprehension notation,
| :{Y ∣ E}× W ≡ {Y× W ∣ EW} ↣ Y× W. |
This is functorial with respect to
| g:W1→ W2, where {Y ∣ E}× g ≡ |
|
(recall that id{Y ∣ E}=E) and to
| :{Y1 ∣ E1}→{Y2 ∣ E2}, where |
| × W ≡ |
| . |
Proof Apply (−)W to the equations in Definition 4.2 to get JW;Σu× W=id and
| Σv× W;JW;Σu× W = Σv× W;JW;Σv× W. |
Proposition 4.14 said that the formal pairs are equalisers, which property commutes with products. In comprehension notation, Σv× W;JW=EW.
The formula for {Y ∣ E}× g is merely naturality of E(−).
Using the injectivity of Y2, we may write F as
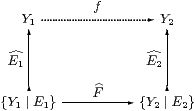
for some (not necessarily unique) f, where (by Definition 4.5) F=F;E2=E1;f, so F=Σf;E1. Applying (−)× W to the commutative square, the formula for F× W has to be E1;(f× W)=G where G≡(Σf;E1)W=FW. ▫
Remark 5.9 Alternatively,
one could show directly that Eg and FW are morphisms,
and that they satisfy the equations for the product functor.
For FW, we need to use the strength
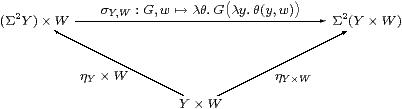
for the monad, which is a natural transformation and obeys the equation shown.
Remark 5.10 The product of two Σ-split pairs
must form a pullback (intersection) in S, in the same way that the
product of any two maps in a category gives rise to a pullback.
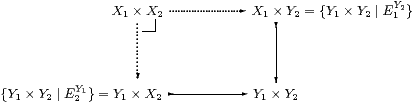
Unfortunately, our “comprehension” notation does not admit intersections — either abstractly or in the leading example of LKLoc — so we still have to find an E on Y1× Y2 to describe the subspace. If E1Y2 and E2Y1 commute (as they do if E1=Σe1 or E2=Σe2) then their composite encodes the intersection. But it turns out that, even if E1Y2;E2Y1≠ E2Y1;E1Y2, either of them will do the job: of course products and pullbacks are unique up to isomorphism, but we have two representations of them.
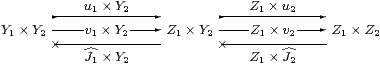
is an object of S, where
|
the inclusion on the last line being in the sense of Notation 4.4.
Proof Clearly u;J=id, whilst
|
Using the given equations of the form vi;Ji;ui=vi;Ji;vi, we must prove this equation for the new Σ-split pair:
|
using centrality of u2, and the same argument with v in place of u.
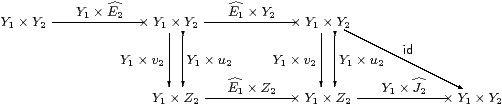
Finally, Y1×E2;E1× Y2;Y1×E2 = Y1×E2;E1× Y2 by centrality of u2 and v2 with respect to E1, and u2;J2=id. ▫
Proposition 5.12
The category S has finite products, where
| {Y1 ∣ E1}×{Y2 ∣ E2} = {Y1× Y2 ∣ E1Y2;E2Y1}, |
whilst the product of the morphisms F1:X′1→ X1 and F2:X′2→ X2 is F1Y′2;F2Y1.
Moreover, the functor S→S takes products in S to products in S.
Proof First consider the product of two objects X1,X2∈obS, expressed in S by means of their standard resolutions, so the products Σ2 X1×Σ2 X2 etc. are preserved (Lemma 5.7). The formal product of the Σ-split pairs (Lemma 5.11) provides an equaliser in S (Proposition 4.14), which is the required product, isomorphic to X1× X2, i.e. this is preserved.
The construction is then applicable to any two Σ-split pairs, so all binary products exist in S. Functoriality follows from that in Lemma 5.8. ▫
Remark 5.13 The abstract situation of idempotents
є ≡ (E2)Y1 and є′ ≡ (E1)Y2
(in this case on the object ΣY1× Y2)
such that є;є′ and є′;є are also idempotent
is studied in Lemma D 7.1.
It is shown there that the splittings of
є;є′ and є′;є
are isomorphic and form a pushout diagram,
in our case of the algebras ΣX1× X2 etc.
corresponding to objects in the above pullback.


