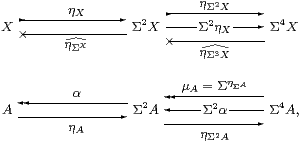



A perhaps more obvious way to construct the monadic completion of S (as I did in 1993) is to consider the algebras, and in fact S≃AlgKSop does the job. As in other approaches, the central difficulty remains that of binary products in S, i.e. coproducts of algebras. For convenience, we assume in this section alone that idempotents split in S, so KS≃S.
The equivalence S≃Algop says that every algebra (A,α) is to be (ΣX,ΣηX) for some new object X∈obS (Definition 3.1). This means that we have to prove properties of A on the basis of its algebra structure that would be obvious if we already knew that A=ΣX. The key such property turns out to be the double exponential transposition,
| Alg(ΣA,B) = |
| (Y,ΣX) ≅ |
| (X,ΣY) = Alg(ΣB,A), |
where X and Y are the S-objects corresponding to the algebras A and B, and ΣX corresponds to ΣA because the functor S→S is supposed to preserve Σ(−).
In effect, using algebras means that we insist on representing each S-object in “normal form” by means of its standard resolution
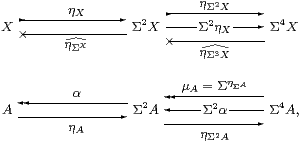
whereas Section 4 was much more flexible about Σ-split pairs. For example, Lemma 5.8 gave the obvious formula for (Y⇉ Z)× W, but this does not take standard resolutions to standard resolutions: the structure map αW that it provides must be composed with a map
| Σ τΣX,W: Σ ΣΣ(X× W) →Σ (ΣΣX× W). |
When we generalise from ΣX to A, we must replace ΣX× W by AW.
Remark 7.1
For any algebra (A,α) and object W,
the object AW splits the idempotent EW, where A itself splits
E≡α;ηA.
Then AW carries a power algebra structure,
ΣτA,W;αW, where the natural transformation
| τA,W:W×ΣA→ΣAW by x,φ↦λ f.φ(f x) |
plays a similar role to that of the strength σ of the monad (Remark 5.9). If H:A→ B is a homomorphism them so is HW:AW→ BW, by naturality of τ(−),W. ▫
In fact, for any strong monad T whose algebras are exponentiable, an algebra structure T(AW)→ AW is given by the transpose of
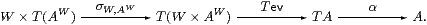
Remark 7.2
When X and Y are expressed by means of the standard resolution,
the pullback in Remark 5.10 is as shown on the left.
As ΣX×Σ2 Y=(ΣX)(Σ2 Y)=AΣB,
the corresponding diagram in Alg is the one on the right,
and is to be a pushout of homomorphisms.
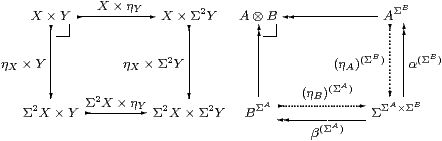
As often happens when we consider algebras, the homomorphisms on the bottom and right are split by functions, the two idempotents in Remark 5.10 being E1ΣB and E2ΣA, where E1≡α;ηA and E2≡β;ηB. When we construct the pushout, we shall find that the other two maps are also split, with the result that the pushout of functions, like the coequalisers that we have used, is absolute. In particular, Σ2(A⊗ B) is also a pushout, enabling us to define the algebra structure Σ2(A⊗ B)→(A⊗ B).
(The reason for using the symbol ⊗ for the coproduct of algebras is simply that the corresponding construction in locale theory is a tensor product of the underlying join semilattices.)
That is the plan for the later parts of the construction, but it also provides the idea for the central technical result. The composite BΣA→ΣΣA×ΣB→ AΣB takes G to λψ.α(λφ.ψ(Gφ)). We now make use of the corresponding external transformation. For A=ΣX and B=ΣY, this is just the double exponential transposition S(ΣΣX,ΣY)≅S(ΣΣY,ΣX).
Lemma 7.3
G↦ΣG;α and F↦ΣF;β
restrict to a bijection Alg(ΣA,B)≅Alg(ΣB,A)
that’s natural with respect to homomorphisms.
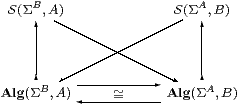
Proof Whatever G is, F≡ΣG;α is a homomorphism, being a composite of two homomorphisms. If G is itself a homomorphism then ΣF;β=Σα;ΣΣG;β=ΣηB;G=G. Given homomorphisms u:A→ A′ and v:B→ B′, the correspondence takes Σv;F;u to Σu;G;v. ▫
Remark 7.4
We can define an internal notion of “object of homomorphisms”
(which should also have its own notation) by interpreting the
external Eilenberg–Moore equation as the equaliser
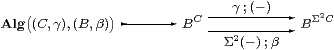
or by a generalisation of the equaliser in Proposition 3.2 with B in place of Σ.
The argument in the Lemma internalises, to show that Alg(ΣA,B) is a split equaliser (retract) of BΣA. Moreover, it is isomorphic in S to Alg(ΣB,A), and we write A⊗ B for either of them. The same argument shows that A⊗ B is an absolute pushout in S, whence it carries a unique algebra structure that makes it a pushout of algebras. ▫
From the external result we can deduce Lemma 5.7, that S→S preserves products of injectives (actually, just carriers of algebras, but that’s no handicap).
Lemma 7.5
If C,D∈obS are carriers of algebras then
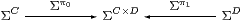
is a coproduct diagram of algebras.
Proof For any other algebra Θ (playing the role of ΣΓ in Section 5),
| Alg(ΣC,Θ)×Alg(ΣD,Θ) ≅ Alg(ΣΘ,C)×Alg(ΣΘ,D) ≅ Alg(ΣΘ,C× D) ≅ Alg(ΣC× D,Θ) |
using Lemma 7.3 three times. Lemma 5.5 gave the algebra structure on C× D. ▫
Corollary 7.6
The algebra ΣΣA×ΣB
has the universal property that
| S(A,Θ)×S(B,Θ) ≅ Alg(ΣΣA×ΣB, Θ). |
Proof Put C≡ΣA and D≡ΣB and recall that S(A,Θ)≅Alg(ΣΣA,Θ). ▫
Next we prove that the power algebra does the job for which it was introduced in Remark 7.1. Here A and D play the roles of Σ{Y ∣ E} and W in Lemma 5.8
Lemma 7.7 For algebras A and D,
the diagram A→ AD ← ΣD is a coproduct of algebras.
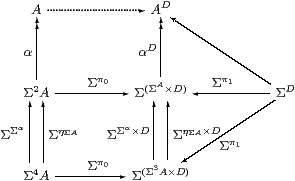
Proof The left-hand column is a U-split coequaliser of algebras, i.e. an absolute coequaliser in S, which the functor (−)D therefore preserves. So the middle column is a coequaliser of (power) algebras, in which the middle and bottom objects are coproducts by Lemma 7.5. But the universal properties of coproducts and coequalisers commute, cf. products and equalisers in Lemma 5.8. ▫
Corollary 7.8
The algebra AΣB has the universal property that
| Alg(A,Θ)×S(B,Θ) ≅ Alg(AΣB, Θ). ▫ |
Theorem 7.9 A⊗ B carries the structure of the coproduct of the
algebras A and B.
Proof By Remark 7.2, A⊗ B is an absolute pushout of the diagram in S, so there is a unique algebra structure on it that makes this diagram a pushout in Alg.
Hence we have isomorphic pullbacks in Set,
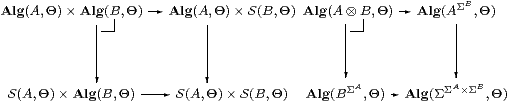
or, in plain English, if the functions A→Θ and B→Θ are actually both homomorphisms then they correspond to a homomorphism from A⊗ B. Therefore this has the universal property of the coproduct. ▫
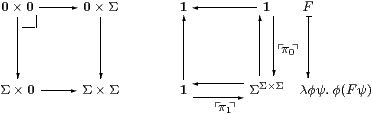
Example 7.10 Recall that any idempotent defines a partition
and chooses an element from each equivalence class.
In this case the two partitions are the same
but the choices of elements are different.
For example in the simplest case, A≡ B≡1,
the two representations are embedded
as the singletons {⌜π0⌝} and {⌜π1⌝}
in ΣΣ2.
Proposition 7.11 Powers of Σ (as we write it) in S≡Algop
are given by
| (A,α)≡(ΣA,ΣηA) and η(A,α)≡α, where |
| ≡(ΣΣ,Ση1). |
Proof Since A⊗ B was defined to have Alg(ΣA,B) as its set of global elements,
| (Γ× X,Σ) = Alg(ΣΣ,A⊗ B) = S(1,A⊗ B) = Alg(ΣA,B) = |
| (Γ,ΣX) |
where A≡ΣΓ and B≡ΣX. ▫
Remark 7.12 For the other structure in terms of algebras,
The last part says that S=Algop is monadic, and therefore admits subspaces as described in Sections 3 and 6, since we assumed that idempotents split in S. ▫


