



What has happened to the “finite open sub-cover” property? Somehow, the underlying ideas of ASD are already robust enough to allow us to develop the basic results about compactness, without mentioning finiteness. On the other hand, we can only define some rather trivial examples of compact spaces.
We need two more axioms to complete our theory. They say explicitly that all functions are Scott-continuous, and that [0,1]⊂ℝ is compact in the sense of the previous section. These ideas were motivated by the infinitary and finitary parts respectively of the discussion of compactness in Notation 2.14. Our goal in this section is to use them to show that the compact subspaces of ℝ are exactly the closed and bounded ones.
Axiom 9.1 For any type X,
every term F:ΣΣX is
Scott-continuous, i.e. it preserves directed joins,
cf. Proposition 3.13.
As we explained following Axiom 5.10, a join indexed by i:I in the space ΣX is an existentially quantified predicate, λ x.∃ i.θ(x,i). To state the Axiom in its general form, the object I must be therefore be overt, and in practice we take it to be discrete too. See Axiom I 4.21 for this general definition of directed joins in ASD.
However, we don’t usually need the generality in this paper because, for a great many of the issues of real analysis, it is enough to consider joins indexed by the arithmetical order on ℕ or ℚ, as we observed in Remark 3.15.
Definition 9.2 A directed relation on a space X
is a predicate θ(x,i)
with x:X, i:ℕ, ℚ or ℝ, and maybe other parameters,
that preserves or reverses the arithmetical order in the second argument,
in one or other of the following senses:
|
We adopt the notation on the right from pre-axiomatic analysis because it is a useful mnemonic, not because i “tends” towards anything. It can easily be generalised to i↗ a or i↘ a.
As we saw earlier, such a relation corresponds to a semicontinuous function from X, or a ℚ-indexed family of open subsets of it. When the “finite open sub-cover” property of a compact space K is used in familiar ways in real analysis, we shall see that a relation like this lies at the core of the argument. As Proposition 10.10 illustrates, the order-preserving property is usually obvious from the form of θ.
Proposition 9.3
Let θ(x,i) be a directed relation on a space X,
where i:ℕ or ℚ.
Then any F:ΣΣX satisfies the rule

|
or
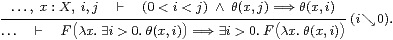
|
Proof In the first case, the indexing space is ℕ or ℚ with the arithmetic order, which the binary operation max makes directed. The second case uses {i:ℚ ∣ i> 0} with the reverse order and min. ▫
We shall see in Corollary 10.3 that these rules are also valid with real instead of rational values of i.
Although this result holds for any functional F on any space X, the most important application is to the necessity operator ▫ or quantifier ∀ for a compact subspace K⊂ X in the sense of the previous section. Then we have the following uniformity principle.
Corollary 9.4 For any directed relation θ(k,i)
on a compact space K,
|
We can say things like this exactly because ours is a logic for topology and not set theory (Remark 5.1), but in order to exploit this principle in real analysis, we need to state the final axiom:
Axiom 9.5 The closed interval
[0,1]⊂ℝ is compact.
The closed subspace [0,1] is co-classified by ω x≡(x< 0)∨(1< x), by definition, so we are now saying that it also has a modal operator ▫ for which the pair (▫,ω) satisfies Definition 8.1. This is unique by Proposition 1.
There’s nothing special about 0 and 1 in this:
Proposition 9.6 The closed interval [d,u]⊂ℝ,
whose endpoints d,u:ℝ may be variables or expressions with parameters,
is the closed subspace co-classified by
| ω x ≡ x< d∨ u< x, |
and is a compact subspace, with
| [d,u]φ ≡ ∀ x:(d≤ x≤ u).φ x ≡ ∀ t:[0,1].φ(d(1−t)+u t). |
Proof This is an application of Theorem 8.9 and Remark 8.17. ▫
It is a serendipitous notational coincidence that the bracket notation [d,u] serves for both the compact subspace and its modal operator.
Remark 9.7
All compact subspaces of ℝ are closed, by
Proposition 8.7, so the next question is whether,
given a closed subspace, it is compact iff it is bounded.
However, the meaning of “boundedness” requires some care,
especially when we allow parameters.
By the definition of ∀K, the compact subspace K is contained in the open interval (d,u), where d and u may be either variables or general real-valued expressions, but nevertheless specified ones, iff
| ∀ x:K.(d< x< u). (a) |
Since this is a proposition, we may quantify d and u (if they’re variables rather than expressions). So K is bounded with unspecified bounds iff
| ∃ d u.∀ x:K.(d< x< u). (b) |
Then (a⇒b) by Axiom 5.10, and Remark 6.6 makes them equivalent, but only when the parameters in the definition of [K] are (at worst) integers or rationals, not real or logical.
Since properties (a,b) use the universal quantifier, we can only state them if we already know that the subspace is compact. On the other hand, the closed subspace co-classified by ω is contained in the open interval (d,u) iff this interval and the complementary open subspace cover ℝ, i.e.
| …, x:ℝ ⊢ (d< x< u)∨ ω x ⇔ ⊤, or λ x.(d< x< u)∨ω x = ⊤:Σℝ. (c) |
It is contained in the closed interval [d,u] iff its complement contains the complement of this interval (cf. Proposition 3.9), i.e.
| …, x:ℝ ⊢ (x< d)∨(u< x) ⇒ ω x, or λ x.(x< d)∨(u< x) ⊑ ω:Σℝ. (d) |
The versions of (c,d) on the left (with x free) are judgements (Axiom 5.2), whilst those on the right (with x bound by λ) are statements (Definition 4.5), to neither of which does the ASD calculus in Section 5 allow us to apply an existential quantifier.
Exercise 9.8 Show that (a ⊢ c ⊣⊢ d).
For [a ⊢ d], we need
| (∀ x:K.d< x< u) ∧ (y< d∨ u< y) =⇒ ω y ≡ (∀ x:K.x≠ y). |
For [c ⊢ d], use Axiom 5.6. The converse, [d ⊢ c], is more difficult, since we need to enlarge the interval: choosing d′< d and u< u′; see Exercise I 6.17 for how to mix < and ≤ in ℝ, and in particular how to deal with d′< d≤ x≤ u< u′. ▫
Once again, we can solve the problem of how to avoid specifying the bounds by generalising the Euclidean reals d and u in property (d) to ascending and descending ones, δ and υ:
Definition 9.9
Let δ and υ be respectively ascending and descending reals
in the sense of Definition 6.7,
except that we do not yet require them to be disjoint or located
(cf. Corollary 9.12).
Then we write [δ,υ]⊂ℝ
for the closed interval (subspace)
that is co-classified by δ∨υ.
We say that another closed subspace, co-classified by ω,
is bounded if there are δ and υ with
| ∃ d u.δ d∧υ u and δ∨υ⊑ω:Σℝ. (e) |
Lemma 9.10
If δ and υ are rounded and bounded
(Definition 6.7) then the
closed interval [δ,υ] is compact, with modal operator
| ▫φ ≡ ∃ d u.δ d∧υ u∧ ∀ y:[d,u].(δ y∨φ y∨υ y). |
Proof As in Definition 8.1, from ▫ we first define
|
which follows from relative instantiation (Proposition 8.2(d)) for [d,u]. Conversely, since δ and υ are bounded there are some d and u with δ d∧υ u, so by Theorem 8.13,
| δ x∨υ x =⇒ ∃ d u.δ d∧υ u∧ ∀ y:[d,u].(δ y∨(x≠ y)∨υ y) ≡ ω x. |
For Definition 8.1, we need φ∨ω≡δ∨φ∨υ⇔⊤ ⊣⊢ ▫φ, in which ⊢ follows from boundedness and ∀ I, and ⊣ from roundedness. ▫
The modal operator ▫ for the interval [δ,υ] has a simpler expression:
Proposition 9.11 ▫φ ⇔ [δ,υ]φ ≡
∃ d u.δ d∧υ u∧ ∀ x:[d,u].φ x.
Proof In the special case where δ≡δe≡λ d.d< e and υ≡υt≡λ u.t< u,
|
We can extend this to the general case by using (general) Scott continuity of the formula Fδυ≡▫φ with respect to δ and υ, with φ as a parameter:
|
and the implication is reversible by monotonicity. ▫
Corollary 9.12
The interval [δ,υ] is occupied iff
δ and υ are disjoint in the sense that
| δ d ∧ (u< d) ∧υ u ⇔ ⊥, |
cf. Lemma I 7.5, but empty iff they overlap.
Proof We have ▫⊥
≡ ∃ d u.δ d∧υ u∧∀ x:[d,u].⊥
⇔ ∃ d u.δ d∧υ u∧(d> u).
This is ⊥ iff δ and υ are disjoint in the sense given,
and ⊤ iff they overlap. ▫
Now we are able to clarify the issues in Remark 9.7.
Proposition 9.13
Every (parametric) compact subspace of ℝ is bounded in the sense
of Definition 9.9.
Proof Given the modal operator ▫ of a compact subspace K, let
| ω x ≡ ▫(λ k.x≠ k), δ d ≡ ▫(λ k.d< k) and υ u ≡ ▫(λ k.k< u), |
so δ∨υ⊑ω, whilst δ is lower and υ is upper.
In order to show that ∃ u.υ u, we use uniformity with respect to the directed relation θ(x,u)≡(x< u) as u↗∞, cf. Remark 3.15; the left-hand side holds with u≡ k+1:
| ⊤ =⇒ ▫(λ k:K.∃ u:ℝ.k< u) =⇒ ∃ u:ℝ.▫(λ k:K.k< u). |
Then υ is rounded because, by Corollary 9.4,
|
Similarly, δ is rounded lower and bounded, and we may choose d and u so that δ d∧(d< u)∧υ u. Hence δ and υ satisfy Definition 9.9. ▫
Remark 9.14 The supremum of the compact
subspace need not exist as a real number (Dedekind cut),
but υ provides it as a descending real.
This is the intersection of the families of upper bounds of the elements of K:
we may form an infinitary intersection of open subspaces like this
because it is indexed by a compact set.
Since, for descending reals, the intrinsic order with which
we form this intersection is the opposite of the arithmetical order
(Remark 3.10),
we have the supremum of K, as in Remark 1.
Theorem 9.15 Any closed subspace of ℝ is compact
iff it is bounded.
Proof By Theorem 8.15 and Propositions 9.11 and 9.13. ▫
Remark 9.16 Notice that each direction of the proof uses one of the two axioms
introduced in this section, so let’s say something about their necessity.
To do this we have to say what we mean by “the real line” in settings that are very different from topology. We take ℝ to be the object of “Dedekind reals” that is defined in Remark I 6.9 as an equaliser of exponentials. This exists in each of the following categories:
Note that we are only saying that these categories obey all but one of the axioms that are stated in this paper: the full (current) ASD theory is stronger than this.
In Russian Recursive Analysis and Bishop’s Constructive Analysis (b) also fails [BR87]. You may therefore be surprised that ASD has both the Heine–Borel theorem and a computable interpretation. This is explained in Section I 15.


