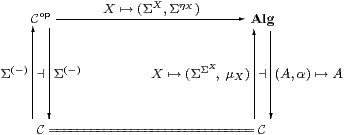



Our new notion of sobriety, expressed in terms of the λ-calculus rather than lattice theory, is a weaker form of the fundamental idea of the abstract Stone duality programme.
Definition 4.1
When the category C of types of values is dual to
its category Alg of algebras of observations,
we say that (C,Σ) is monadic.
More precisely, the comparison functor Cop→Alg
defined by Lemmas 3.3 and 3.6,
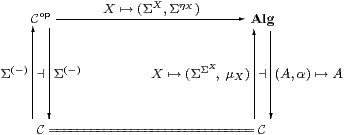
(which commutes both with the left adjoints and with the right adjoints) is to be an equivalence of categories, i.e. full, faithful and essentially surjective.
Remark 4.2
It is possible to characterise several weaker conditions than
categorical equivalence, both in terms of properties of the objects of C,
and using generalised “mono” requirements on ηX.
In particular,
the functor Cop→A is faithful iff all objects are “ T0”
(cf. Remark 1.13),
and also reflects invertibility iff they are replete
[Hyl91, Tay91].
Another way to say this is that each ηX is mono or extremal mono,
and a third is that Σ is a weak or strong cogenerator.
For example, ℕ with primitive recursion is T0 so long as the calculus is consistent, but repleteness and sobriety are equivalent to general recursion [for decidable predicates] (Sections 9–10).
In this paper we are interested in the situation where the functor is full and faithful, i.e. that all homomorphisms are given uniquely by Lemma 3.6. We shall show that the corresponding property of the objects is sobriety, and that of ηX is that it be the equaliser of a certain diagram.
Lemma 4.3
Let (A,α) be an algebra, Γ any object
and H:A→ΣΓ any map in C.
Then H is a homomorphism iff its double exponential transpose
P:Γ→ΣA (Proposition 2.11) has equal composites
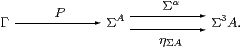
Proof We have H=ηA;ΣP and P=ηΓ;ΣH. [⇒] P;Σα=ηΓ;ΣH;Σα=ηΓ;Σ2ηΓ;Σ3 H =ηΓ;ηΣ2 Γ;Σ3 H=ηΓ;ΣH;ηΣ A =P;ηΣ A. [⇐] α;H=α;ηA;ΣP=ηΣ2 A;Σ2α;ΣP =ηΣ2 A;ΣηΣ A;ΣP=ΣP =Σ2ηA;ΣηΣ A;ΣP =Σ2ηA;Σ3 P;ΣηΓ=Σ2 H;ΣηΓ. ▫
Corollary 4.4
The (global) elements of the equaliser are the those functions
A→Σ that are homomorphisms. ▫
Definition 4.5 Such a map P is called prime.
(We strike through the history of uses of this word, such as in
Definition 1.7 and Corollary 5.8.
In particular, although the case X=ℕ will turn out to be
the most important one, we are not just talking about
the numbers 2, 3, 5, 7, 11, ...!)
As we always have A=ΣX in this paper,
we usually write P as a term Γ⊢ P:ΣΣX.
Lemma 4.6
In Lemma 4.3, ηX is the prime
corresponding to the homomorphism id:ΣX→ΣX.
If P:Γ→ΣA is prime and J:B→ A a homomorphism
then P;ΣJ is also prime.
In particular, composition with Σ2 f preserves primes.
▫
Definition 4.7
We say that an object X∈obC is sober if the diagram
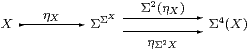
is an equaliser in C, or, equivalently, that the naturality square
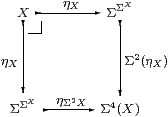
for η with respect to ηX is a pullback.
Remark 4.8 We have only said that
the existing objects can be expressed as equalisers,
not that general equalisers can be formed.
In fact, this equaliser is of the special form described below,
which Jon Beck exploited to characterise monadic adjunctions
[Mac71, Section VI 7], [BW85, Section 3.3],
[Tay99, Section 7.5].
The category will be extended to include such equalisers,
so we recover a space pts(A,α) from any algebra,
in [B].
Notice the double role of Σ here, as both a space and an algebra. Peter Johnstone has given an account of numerous well known dualities [Joh82, Section VI 4] based the idea that Σ is a schizophrenic object. (This word was first used by Harold Simmons, in a draft of [Sim82], but removed from the published version.)
Moggi [Mog88] called sobriety the equalizing requirement, but did not make essential use of it in the development of his computational monads.
Applegate and Tierney [Eck69, p175] and Barr and Wells [BW85, Theorem 3.9.9] attribute these results for general monads to Jon Beck. See also [KP93] for a deeper study of this situation.
Proposition 4.9 Any power, ΣU, is sober.
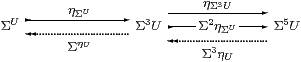
Proof This is a split equaliser: the dotted maps satisfy
|
by Lemma 2.10, the equations on the right being naturality of η with respect to ΣηU and ηΣU. Hence if P:Γ→Σ3 U has equal composites then P=P;ΣηU;ηΣU, and the mediator is P;ΣηU. ▫
Theorem 4.10
The functor Σ(−):Cop→Alg given in Definition 4.1
is full and faithful iff all objects are sober.
Proof [⇒] We use P:Γ→Σ2 X to test the equaliser. By Lemma 4.3, its double transpose H:ΣX→ΣΓ is a homomorphism, so by hypothesis H=Σf=ηΣX;ΣP for some unique f:Γ→ X, and this mediates to the equaliser.
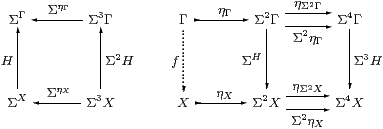
[⇐] Let H:ΣX→ΣΓ be a homomorphism, so the diagram on the left above commutes, as do the parallel squares on the right, the lower one by naturality of Ση with respect to H. Since X is the equaliser, there is a unique mediator f:Γ→ X, and we then have H=ηΣX;ΣP=ηΣX;ΣηX;Σf=Σf. ▫
Remark 4.11
Translating Definition 1 into the λ-calculus,
the property of being a homomorphism H:ΣX→ΣU
can be expressed in a finitary way
as an equation between λ-expressions,
| F:Σ3 X⊢(λ u.F(λφ.Hφ u)) = H(λ x.F(λφ.φ x)), |
the two sides of which differ only in the position of H.
The double exponential transpose P of H is obtained in the λ-calculus simply by switching the arguments φ and u (cf. Remark 1.11). Hence ⊢ P:U→ΣΣX is prime iff
| u:U, F:Σ3 X ⊢ F(P u) = P u(λ x.F(λφ.φ x)). |
Replacing the argument u of P by a context Γ of free variables, Γ⊢ P:ΣΣX is prime iff
| Γ, F:Σ3 X ⊢ F P ⇔ P(λ x.F(λφ.φ x)) |
or F P ⇔ P(ηX;F). This is the equation in Lemma 4.3, with A=ΣX, applied to F.
[In the context of the additional lattice structure, including Scott continuity, P is prime iff it preserves ⊤, ⊥, ∧ and ∨ Theorem G 10.2.]
Corollary 4.12 The type X is sober iff
for every prime Γ⊢ P:Σ2 X
there is a unique term Γ⊢focusP:X such that
| Γ, φ:ΣX ⊢ φ(focusP) ⇔ Pφ. |
Hence the side-condition on the introduction rule for focusP in Remark 2.12 is that P be prime. Indeed, since φ↦φ x is itself a homomorphism (for fixed x), this equation is only meaningful in a denotational reading of the calculus when P is prime. (On the other hand Thielecke’s force operation has this as a β-rule, with no side condition, but specifies a particular order of evaluation.) ▫
Remark 4.13 So far, we have used none of the special structure on Σ in
Remarks 2.4ff. We have merely used the restricted
λ-calculus to discuss what it means for the other objects of
the category to be sober with respect to it.
In Sections 6–8
we shall show how to enforce this kind of sobriety on them.
If P=ηX(x) then the right hand side of the primality equation easily reduces to the left. Otherwise, since F is a variable, the left hand side is head-normal, and so cannot be reduced without using an axiom such as the Euclidean principle (Remark 2.4), as we shall do in Proposition 10.6.
The introduction of subspaces [B][E] also extends the applicability of the equation, by allowing it to be proved under hypotheses, whilst using the continuity axiom (Remark 2.6) it is sufficient to verify that P or H preserves the lattice connectives. In other words, the mathematical investigations to follow serve to show that the required denotational results are correctly obtained by programming with computational effects.
Remark 4.14 In his work on continuations, Hayo Thielecke uses R
for our Σ and interprets it as the answer type.
This is the type of a sub-program that is called like a function,
but, since it passes control by calling another continuation,
never returns “normally” — so the type of the answer is irrelevant.
Thielecke stresses that R
therefore has no particular properties or structure of its own.
In the next section, we shall show that the Sierpiński space in topology behaves categorically in the way that we have discussed, but it does carry additional lattice-theoretic structure.
Even though a function or procedure of type void never returns a “numerical” result — and may never return at all — it does have the undisguisable behaviour of termination or non-termination. Indeed, we argued in Remark 1.2 that termination is the ultimate desideratum, and that therefore the type of observations should also carry the lattice structure. Proposition 10.6, which I feel does impact rather directly on computation, makes use of both this structure and the Euclidean principle.
[The referee pointed out that there are, in practice, other computational effects besides non-termination, such as input–output.]
Thielecke’s point of view is supported by the fact that the class of objects that are deemed sober depends rather weakly on the choice of object Σ: in classical domain theory, any non-trivial Scott domain would yield the same class.
Remark 4.15 Although it belongs in general topology, sobriety was first
used by the Grothendieck school in algebraic geometry
[AGV64, IV 4.2.1]
[GD71, 0.2.1.1] [Hak72, II 2.4].
They exploited sheaf theory, in particular the functoriality of
constructions with respect to the lattice of open subsets, the points
being secondary.
An algebraic variety (the set of solutions of a system of polynomial equations) is closed in the Euclidean topology, but there is a coarser Zariski topology in which they are defined to be closed. When the polynomials do not factorise, the closed set is not the union of non-trivial closed subsets, and is said to be irreducible. A space is sober (classically) iff every irreducible closed set is the closure of a unique point, known in geometry as the generic point of the variety. Such generic points, which do not exist in the classical Euclidean topology, had long been a feature of geometrical reasoning, in particular in the work of Veronese (c. 1900), but it was Grothendieck who made their use rigorous.


