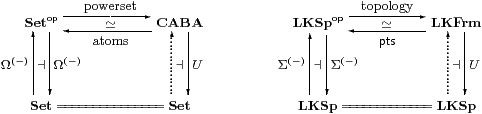


The existence or otherwise of extensional subspaces is a point of demarcation between pure mathematics and computer science. The ubiquitous axiom of comprehension seems to be what mainstream mathematicians have in mind when they insist that Set Theory provides the foundations of their subject. On the other hand, neither programming languages nor the type theories that are most popular in computer science admit subtypes. (We do not mean the notion of this name in object-oriented programming, which is like an extension of the signature of an algebraic theory.) Subtypes in our sense are used in software development, in the form of Floyd–Hoare logic, with pre- and post-conditions, but it is an up-hill struggle to teach programmers to use them!
The reason for this demarcation is that the essence of the development in a mathematical argument is quite different from that in a computation. Before the referee will allow me to say that an element belongs to a subset, I must prove that it satisfies the defining property. Otherwise, the rest of the argument has no meaning whatever, and my paper is not published. From this point of view, compilation of high level programming languages lies on the mathematical side of the boundary. A (low level) computation, on the other hand, proceeds irrespectively of whether or not a purported mid-condition is satisfied: if it doesn’t, the behaviour of the program may not be what the programmer had in mind, but it nevertheless does something.
I am, of course, in favour of constructive mathematics, and appreciate the analogy between programs and proofs, but opinions differ as to what is regarded as constructive: my notion is stronger than Johnstone’s [Joh82] but weaker than Martin-Löf’s [ML84]. I have argued that what Per Martin-Löf calls the “existential quantifier” and the “axiom of choice” are not those used in geometry [Tay99, Section 2.4], and nor do I consider that an element of a subset needs to be accompanied by a proof of the defining predicate. Such proofs may serve as guarantees, but at some point we must eventually trust (the verification of) the guarantee and carry on with the computation.
In crossing the demarcation from pure mathematics to programming, we therefore have to extend the definition of functions that were intended to be defined on a subset to the whole of the ambient set, possibly at the cost of results that lie outside the intended target. A target object that permits such extension without itself being expanded is called injective, and such objects will play an important role in this paper.
I see the crossing as building a “mathematically comfortable” platform, with more types (sets, spaces) than the underlying programming language, but such that the terms (elements) become programs when the richer type information is erased. The programming language that we shall use was justified and developed in the previous paper [A], so now we must consider ways of building mathematical platforms. Category theory provides the language in which to express both our requirements for “comfort” and the means of satisfying them, although equivalent λ-calculi are needed for the idioms of both mathematics and programming.
Programming languages include constructors for making new types from old ones, but the additional mathematical types depend on terms. A very general theory of such dependent types is formulated in [Tay99, Chapter VIII], although I now consider that to be too complicated. Simpler notions than the axiom of comprehension are familiar in category theory: equalisers, pullbacks, coequalisers and pushouts.
The present work is by no means the first to provide such extensions. One very simple idea is to split idempotents (Remark 4.1), which Dana Scott developed [Sco76]. However, a great deal of artificiality was piled on top of this, notably sum types with spurious additional elements: we shall find in Section 11 that stable disjoint coproducts are a mathematical comfort that we may reasonably demand as standard.
Another idea is to expand the monoid of (partial general) recursive functions on ℕ to the category whose objects are recursively enumerable subsets. Giuseppe Rosolini formulated the abstract notion of partial maps (composing a p-category), and constructed a category with subobjects from it [Ros86]. Peter Freyd and Andre Scedrov started instead from binary relations (composing an allegory) [FS90]. Their theory also accounts for the way in which general sets may be obtained from iterated powersets, traditionally known as the von Neumann hierarchy. Bill Lawvere’s treatment [Law70] describes and generalises the behaviour of comprehension in toposes and other categories in which it already exists, but does not explain how it creates new sets [Tay99, Exercises 9.45ff]. Other ways of expanding the class of types include the regular and exact completions of categories.
The particular construction performed in this paper is based on a monad. In the original mathematical development of monads, Eilenberg–Moore algebras were given a preferential role [Eck69, BW85]. Later, Eugenio Moggi demonstrated how they could be used to encode features of computation [Mog91], but the new types that he introduced were objects of the Kleisli category, which consists of just the free algebras. So the literature that has ensued illustrates the demarcation between mathematics and computer science. In particular, the basic form of our construction without the subspaces (Section A 6)1is similar to work of Hayo Thielecke [Thi97a], which uses the the Kleisli category.
In none of these constructions is a type defined as a “collection”, as Solomon Feferman claimed to be a necessary ingredient of mathematical foundations [Fef77], and nor is a subtype a sub-collection selected by some kind of demon. Both the underlying programming language and its mathematical enrichment may be defined as λ-calculi with certain syntactic rules of formation. Of course, there is a (recursive) collection of well formed formulae (or of objects and morphisms in the category), but this cannot be what Feferman’s argument means, as it applies equally to Set Theory itself. The metalanguage of category theory and type theory is not only first order, as is that of Set Theory, but essentially algebraic. In our case, the universal properties of Σ-split (co)equalisers are equational, so the quantifier complexity is even less.
Many of the mathematical intuitions on which our calculus is based come from general topology, regarded as a more subtle form of set theory. This research programme is named after Marshall Stone because he was the first to emphasise that one should always look for the topology on any mathematical object that one has constructed, since the appropriate morphisms are continuous functions, not arbitrary set-theoretic ones à la Cantor. (See the Introduction to [Joh82] for a historical survey of this point of view.)
Contrary to what Richard Dedekind and Georg Cantor have told us, this is how the real line ℝ is defined: we understand the topology Σℝ because this is the abstraction of the convergence of sequences of rationals (or of otherwise algebraically definable numbers), and this is the only way by which we gain access to transcendental numbers [I]. The space ℝ exists by fiat, being defined formally as pts(Σℝ). Indeed, Bourbaki also constructed ℝ at the end of a tortuous chain of definitions that spans an entire volume [Bou66], but essentially recovers it from a topology that is defined in terms of ℚ.
It was Dana Scott who promoted the analogy between continuity and computability. However, there cannot be a precise connection with the traditional axiomatisation of general topology, because it relies on arbitrary unions, rather than recursive ones. It is principally this problem that Abstract Stone Duality seeks to address.
Monads provide a way of handling infinitary algebra of the kind that we need to re-axiomatise topology, and may be defined over any category, not just the category of sets. Specifically, we define the algebras that replace the lattices of open subsets of a space using a monad over the category of spaces itself.
This use of monads was also inspired by Marshall Stone’s work. By Stone duality we understand the dual equivalence between a category of algebraically defined objects and another whose objects we think of as “spaces”, though they may be sets, posets or algebraic varieties as well as topological spaces.
By abstract Stone duality we mean some category S of “spaces” whose opposite category Sop≃A is itself “algebraic” over S in the sense of being the category of Eilenberg–Moore algebras over S.
The analogy between the two concrete examples of sets and locally compact spaces drives the intuition behind this programme. Temporarily using classical logic, including the axiom of choice, to present this intuition, these two monadic situations are illustrated by the following diagrams.
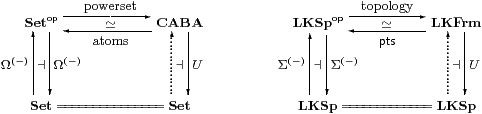
Adolf Lindenbaum and Alfred Tarski characterised full powerset lattices classically as complete atomic Boolean algebras [Tar35]. In modern terms, we formulate their result as a mutually inverse pair of functors, one of which takes a set X to its powerset ℘ X, and the other extracts the set of “atomic” elements of any complete atomic Boolean algebra.
The morphisms of CABA preserve arbitrary meets and joins, and the forgetful functor U:CABA→Set from this category has a left adjoint. The free complete atomic Boolean algebra on a set X is its double powerset, ℘℘ X, and it may be shown that this adjunction is monadic.
The equivalence of categories re-states this concrete adjunction in more abstract terms: the contravariant powerset functor ℘:Setop→Set is self-adjoint, and (since the squares commute) the Lindenbaum–Tarski theorem says that this adjunction is also monadic. Robert Paré proved the same result intuitionistically for any elementary topos [Par74]. Classically, ℘ X≅2X, whilst ℘ X≅ΩX in a topos, where Ω denotes the type of truth values.
In the second diagram, Frm is the category of frames, i.e. lattices with arbitrary joins over which binary meets distribute, and homomorphisms that preserve finite meets and arbitrary joins. Frames are therefore the kind of lattices that open subsets constitute in general topology, whilst the homomorphisms capture the properties of inverse image maps for continuous functions. LKSp and LKFrm are the categories of locally compact sober spaces and the frames that arise as their topologies, namely those that are also continuous lattices [HM81].
LKSp and LKFrm are dual categories, where the “points” of a frame may be characterised lattice-theoretically [Joh82, Section II 1] or by means of an exponential Σ(−) and its associated λ-calculus [A]. Frm is also a category of Eilenberg–Moore algebras for a monad over Set. However, if U forgets just the finitary lattice structure, but leaves the carrier equipped with its directed joins and so the Scott topology, LKFrm is monadic over LKSp.
Again, the monadic adjunction may be seen abstractly, where the powerset ℘ X≅ΩX is replaced by the topology, i.e. the lattice of open subsets of X, and the lattice itself is regarded as a space with the Scott topology. The topology may be expressed as ΣX, where Σ is the Sierpiński space. Classically Σ also has two points, one of which is open.
The theorems of Stone, Tarski and Lindenbaum that we have given identified “atoms” or “points” in the lattices as sets of sets. This turns the set-theoretic membership relation on its head: each “open set” (element of the algebra) belongs to certain “points”, i.e. these correspond to certain subsets of the algebra. However, the existence of enough ideal points to separate the elements of the algebra is equivalent to the axiom of choice, or at least to some weaker proper axiom such as the prime ideal theorem. Just the same problem arises in model theory, models being the “ideal points” of the predicate calculus.
In the following two sections we show how, when the category of “spaces” satisfies the abstract Stone duality, it admits subspaces that carry the subspace topology. This is a special case of Jon Beck’s general characterisation of monadic adjunctions: under the duality, subspaces correspond to quotient algebras, and Beck’s theorem says that we may calculate certain kinds of quotient algebras simply as quotients of their carriers. For textbook accounts of monads and Beck’s theorem, see [Mac71, Section VI 7], [BW85, Section 3.3] or [Tay99, Section 7.5]. Our discussion in Section 3 is partly intended to amplify these accounts by giving a worked example of Beck’s theorem, in the hope that it will cross the demarcation and become better understood in the theoretical computer science community.
Theorem 3.11 gives an intuitionistic proof of Stone duality for locally compact locales. After this, there is no more topology in this paper: that story — in particular, the equivalence between Eilenberg–Moore and frame homomorphisms — is taken up in [C][G].
Sections 4–6 build a new category S with the abstract Stone duality from one that simply has products, powers of Σ and all objects sober. The construction is based directly on Beck’s theorem, formally adding Σ-split equalisers. The main difficulty is in showing that S has products, for which injective objects are needed as a tool.
Section 7 briefly describes an alternative construction that uses algebras instead.
Sections 8–10 investigate an equivalent λ-calculus, whose types admit subspaces that are described using something like the axiom of comprehension in set theory. However, these type annotations, like the mid-conditions in Floyd–Hoare logic, are computationally anodyne: they remain in the journal papers and are not used at run-time. The terms may be stripped of this complex type information, leaving a simple λ-calculus with application and abstraction.
The final section constructs stable disjoint coproducts and Σ-split coequalisers.
Some comment is in order on the fact that locally compact locales, rather than all locales, provide the leading model of our axioms. Fundamentally, it is the category that we seek to axiomatise, not the spaces, and one category has the monadic property, whilst the other doesn’t. Indeed, the axioms for locales hardly enjoy the same unanimous acceptance in the mathematical community as do those for, say, groups. Spatial locales agree with sober spaces, but even then disagree as to their products outside the locally compact case, whilst there are numerous competing axiomatisations of convergence and other features of topology. The traditional one has also long been regarded as unsatisfactory on the grounds that its logical properties (such as cartesian closure) are inadequate. This paper breaks new ground in treating topology as λ-calculus.
The simple technical reason for the “restriction” is that the exponential ΣX is only defined when X is locally compact. However, Steven Vickers has shown how the functor ΣΣ(−) may be extended to all locales, decomposing it into two covariant functors that are of interest in themselves [Vic04a]. However, the Eilenberg–Moore category for his monad is not the category of frames, but one whose opposite he calls the category of colocales. When X is a locale, ΣX is a colocale, and vice versa, so observations belong not merely to a different type from values, but to another category, whilst meta-observations are again like values. Our experience since Turing that computations are ultimately untyped seems to have been sacrificed on the altar of conformity with a pre-existing mathematical structure.
I acknowledge, on the other hand, that my mathematical platform is not as comfortable as we might like. In particular, the intersection of two Σ-split subspaces need not be another locally compact space. Before we are allowed to form an equaliser or coequaliser, we have to satisfy a very awkward property, which turns out to have no computational meaning anyway. (It also leads to mis-conceived questions such as largest cartesian closed categories: the statement that “John is the tallest person who can stand up in here” may say more about the ceiling than about John, if we are talking about children in a tent.) You pays your money, you takes your choice: my construction has a good λ-calculus, whilst locales have (infinitary) algebra, which Vickers’ work has exploited very fluently. Plainly we should be asking for both, and there is no fundamental reason why we shouldn’t have them. The resulting category will have many more objects besides locales and colocales, and will in fact be cartesian closed. So the argument from authority (or at least from familiarity) seems to caution against a too hasty search for generality.
The applications to topology do, unfortunately, go rather quickly outside local compactness. Some account of the category of locales is therefore needed quite urgently in abstract Stone duality, and I hope that Vickers’ work will help towards this. It is possible that such a construction would be the first step of an iteration that would lead to the bigger category, whilst retaining the essence of topology that we distill here. I believe that this lies in the preservation by ΣΣ(−) of certain kinds of equalisers, but more liberal notions of subspace and injectivity will be needed.
Nevertheless, both domain theory and rather a lot of the corpus of pure mathematics may be seen as going on in the category of locally compact spaces, so it is well worth continuing to investigate what can be done in the abstract setting that we have so far.

