14 From the basis to the space

14 From the basis to the space

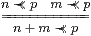
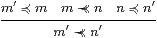
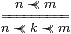
We are now able to show that any “abstract” basis satisfying the conditions of Section 11 actually arises from some definable object. As in Section 12, we have to define a nucleus E:Σ^{Σ^N}→Σ^{Σ^N} and (in the next section) characterise its admissible terms in the sense of Definition 12.8.

Definition 14.1 An abstract basis is an overt discrete object N with elements 0,1∈ N, binary operations +,⋆:N× N→ N and an open binary relation ≺≺:N× N→Σ such that

0≺≺ 0

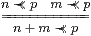
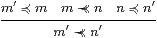
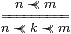
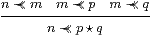
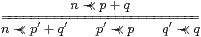
where ≼ is defined from + and ⋆ by Definition 13.10.

Notation 14.2

E	≡	λ Φ.λξ.J(λ n.∃ L.(n≺≺ev L)∧A_L Φ)ξ
	≡	λ Φ.λξ.∃ n.∃ L.ξ n∧(n≺≺ev L)∧A_L Φ.

We have to show that this satisfies the equations in Theorem 10.10,

Φ,Ψ:Σ^{Σ^N} ⊢ E(Φ∧ Ψ) = E(E Φ∧ E Ψ) and E(Φ∨ Ψ) = E(E Φ∨ E Ψ).

This is made a little easier by the fact that we need only test these equations for basic Φ≡ B^R and Ψ≡ B^S:

Lemma 14.3

Proof We use the lattice basis expansion Φ = ∃ R.A_R Φ∧ B^R.

Note first that the combined expansion using distributivity (Lemma 11.8),

Φ ⊙ Ψ = ∃ R S. A_R Φ ∧ A_S Ψ ∧ (B^R⊙ B^S),

is directed in <R,S>, so E preserves the join by Theorem 9.6 and E Φ = ∃ R.A_R Φ ∧ E B^R. Using distributivity, directedness and Scott continuity again, we have

E Φ⊙E Ψ	=	∃ R S. A_R Φ ∧ A_S Ψ ∧ (E B^R⊙ E B^S) distributivity
E(E Φ⊙E Ψ)	=	∃ R S. A_R Φ ∧ A_S Ψ ∧ E(E B^R⊙ E B^S) directedness
	=	∃ R S. A_R Φ ∧ A_S Ψ ∧ E(B^R⊙ B^S) hypothesis
	=	E(Φ⊙ Ψ) ▫

Next we need to evaluate the expression A_L(E B^R).

Lemma 14.4 E B^R = J(λ n.n≺≺ev R).

Proof

E B^R	=	J(λ n.∃ L.n≺≺ev L∧ A_L B^R) Definition 14.2
	≤	J(λ n.∃ L.n≺≺ev L≼ev R) Lemma 13.14
	=	J(λ n.n≺≺ev R) Definition 14.1

but the ≤ is an equality, as we may put L≡ R in the other direction. ▫

Lemma 14.5 Since, by hypothesis, ≺≺ satisfies 0≺≺ k and (cf. Lemma 11.3)

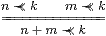
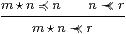
we have A_L(E B^R) ⇒ (ev L≺≺ev R), with equality in the case L≡{|{|k|}|}.

Proof The reason for the inequality is that, whereas B⁽⁻⁾:Fin(Fin N)→DL(N)→Σ^{Σ^N} sends + to ∨ and ⋆ to ∧, A₍₋₎ only takes + to ∧, not necessarily ⋆ to ∨.

A_L(E B^R)	⇔	∀ℓ∈ L.E B^R(λ m.m∈ℓ) def A_L
	⇔	∀ℓ∈ L.J(λ n.n≺≺ev R)(λ m.m∈ℓ) Lemma 14.4
	⇔	∀ℓ∈ L.∃ n∈ℓ.n≺≺ev R def. J
	⇒	∀ℓ∈ L.µℓ≺≺ev R ⋆ rule
	⇔	ev L≺≺ev R 0, + rules

Here µℓ is the “product” of ℓ, in the sense of 1 and ⋆ (written fold ⋆ 1 ℓ in functional programming notation), so n∈ℓ⇒µℓ≼ n. Then ev L is the sum of these products (Definition 13.10). Equality holds when L≡{|{|k|}|} since ℓ={|k|} and ev L=µℓ=k. ▫

Equipped with formulae for E B^R and A_L(E B^R), we can now verify the two equations. Their proofs are almost the same, illustrating once again the lattice duality that we get by putting directed joins into the background. Unfortunately, they’re not quite close enough for us to use ⊙ and give just one proof. First, however, we give the similar but slightly simpler argument for idempotence, although it is easily seen to be implied by either of the other results.

Proposition 14.6 If ≺≺ satisfies the transitive and interpolation rules,

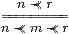
cf. Corollary 11.7, then E is idempotent: E(E Φ)=E Φ.

Proof By (a simpler version of) Lemma 14.3, it’s enough to consider Φ≡ B^R,

E(E B^R)	=	J(λ n.∃ L.(n≺≺ev L)∧ A_L(E B^R)) Notation 14.2
	≤	J(λ n.∃ m.(n≺≺ m)∧ (m≺≺ev R)) Lemma 14.5
	=	J(λ n.n≺≺ev R) hypothesis
	=	E B^R Lemma 14.4

where m≡ev L. However, the ≤ is an equality as we may use L≡{|{|m|}|} in Lemma 14.4 to prove ≥. ▫

Proposition 14.7 Since ≺≺ obeys the rule linking it with ⋆,

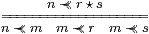
(cf. Lemma 11.11) E satisfies the ∧-equation, E(Φ∧ Ψ) = E(E Φ∧ E Ψ).

Proof By Lemma 14.3, it’s enough to consider Φ≡ B^R and Ψ≡ B^S. With m≡ev L, r≡ev R and s≡ev S,

E(E B^R∧ E B^S)	=	J(λ n.∃ L.(n≺≺ev L)∧A_L(E B^R∧ E B^S)) Notation 14.2
	=	J(λ n.∃ L.(n≺≺ev L)∧A_L(E B^R)∧A_L(E B^S)) Lemma 13.6
	≤	J(λ n.∃ m.(n≺≺ m)∧(m≺≺ r)∧(m≺≺ s)) Lemma 14.5
	=	J(λ n.n≺≺ r⋆ s) hypothesis
	=	J(λ n.n≺≺ev(R⋆ S)) Lemma 13.13
	=	E B^R⋆ S = E(B^R∧ B^S) Lemmas 14.4 & 13.5

To make the ≤ an equality, we use L≡{|{|m|}|} in Lemma 13.14. ▫

Proposition 14.8 If ≺≺ satisfies the Wilker rule linking it with +,

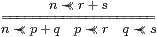
(cf. Lemma 11.12) then E satisfies the ∨-equation, E(Φ∨ Ψ) = E(E Φ∨ E Ψ).

Proof With r≡ev R, s≡ev S, p≡ev L₁, q≡ev L₂ and L=L₁+L₂,

E(E B^R∨ E B^S)	=	J(λ n.∃ L.(n≺≺ev L)∧ A_L(E B^R∨ E B^S)) Notation 14.2
	=	J(λ n.∃ L₁ L₂. (n≺≺ev L₁+ev L₂)∧ A_L₁(E B^R)∧ A_L₂(E B^S)) 13.7
	≤	J(λ n.∃ p q. (n≺≺ p+q)∧ (p≺≺ r)∧ (q≺≺ s)) Lemma 14.5
	=	J(λ n.n≺≺ r+s) hypothesis
	=	J(λ n.n≺≺ev(R+S)) Lemma 13.13
	=	E B^R+S = E(B^R∨ B^S) Lemmas 14.4 & 13.5

Again the ≤ becomes an equality, using L₁≡{|{|p|}|}, L₂≡{|{|q|}|} and L≡ L₁+L₂ in Lemma 13.14. ▫

Theorem 14.9 E is a nucleus on Σ^N in the sense of Section B 8. ▫