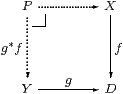



From now on we concentrate on the full subcategory of overt discrete objects, showing that it is a pretopos. The notion of pretopos is the finitary part of Jean Giraud’s categorical characterisation of Grothendieck toposes [Joh77, Theorem 0.45]. These are the properties of the category of “sets” that we require in order to do algebra and symbolic logic in it, for accounts of which see [MR77], [FS90], [Tay99, Chapter V]. In particular we shall show how to construct quotients by equivalence relations using a Σ-split coequaliser.
For point-set topology, related results in both the open and proper cases are to be found in [Bou66, §5.2], except that there an open equivalence relation is by definition one for which q is an open map.
As we do not currently have pullbacks of general open maps (Remark 7.5), we cannot yet develop relative versions of these results for étale maps D→ Z, which Joyal and Tierney define as open maps for which Δ:D→ D×Z D is also open [JT84, §V 5].
Proposition 10.1
Pullbacks rooted at any discrete object D exist.
Proof
▫
Lemma 10.2
If X is an overt object then f and g*f are pre-open maps,
and the Beck–Chevalley condition holds.
Proof (id,f):X↪ X× D and p1:X× D→ D are pre-open maps (Propositions 3.11 and 8.2), where, for φ∈ΣX, ∃(id,f)φ≡ λ x d.φ(x)∧(f x =D d), so
| ∃fφ = λ d. ∃ x. φ(x)∧(f x =D d). ▫ |
Corollary 10.3 If i:X→ D is a mono between overt discrete
objects then X is classified by some φ∈ΣD.
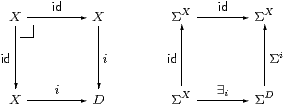
Proof The square on the left is a pullback iff i is mono, and then the Beck–Chevalley condition (Propositions 3.11 and 8.1) makes the square on the right commute (Σi·∃i=id), which was the condition required in Theorem 3.10. [See §O 8.10 for a simpler symbolic proof.] ▫
Definition 10.4 A pre-open map f is surjective
if id=∃f·Σf.
This is equivalent to (∃f⊤)⇔ ⊤ by the Frobenius law, cf. [JT84, §V 4].
Lemma 10.5 Let f be a pre-open surjective map [from
an overt object to a discrete one]. Then g*f is also pre-open surjective.
Proof By the proof of Lemma 10.2, surjectivity of f:X→ D says that
| λ d.⊤=∃fΣf(λ d.⊤)=∃f(λ x.⊤) =λ d.∃ x.(f x=D d), |
which means “∀ d∈ D.∃ x∈ X.(f x=D d)” externally, cf. Remark 8.8.
We require ∃X·∃i·Σi·Σp1=id, where the effect of ∃i·Σi was described in Remark 8.7. This is the case for ψ∈ΣY because (∃ x.ψ y∧(f x=D g y))⇔ (ψ y∧∃ x. f x=D g y)⇔ ψ y by Frobenius and surjectivity of f at d≡ g y. ▫
Proposition 10.6
If X and Y are both overt or both discrete then so is P.
Proof ∃P≡ ∃Y·∃g*f and (=P)≡ (=X)∧(=Y), cf. Propositions 6.11 and 8.3. ▫
Proposition 10.7 For any morphism f:X→ D from an overt object to a discrete one,
the kernel pair K⇉ X of f exists,
and i:K↪ X× X is an open equivalence relation
(reflexive, symmetric and transitive). ▫
Lemma 10.8 Let X be an overt object and i:K↪ X× X
an open equivalence relation classified by δ:X× X→Σ.
Then the coequaliser K⇉ X↠ Q exists in C
and X↠ Q is a pre-open surjection.
[See Example B 11.13 for a construction
using a nucleus in the ASD λ-calculus.
In fact, K can be also constructed as a subspace of ΣX
.]
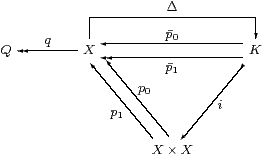
Proof Write p0≡ p0∘ i and p1≡ p1∘ i.
Since the monadic property says that Σ(−):C≃Algop, we calculate the coequaliser q of p0,p1:K⇉ X as the equaliser Σq of the homomorphisms Σp0 and Σp1 in Alg. As monadic forgetful functors create equalisers, it suffices to show that the carrier of this equaliser exists as an object of C when we just consider Σp0 and Σp1 as functions (C-morphisms). To do this we show that ∃p1 splits the equaliser, i.e. that ΣQ is a retract of ΣX, not just a subobject.
The equations to be verified are
| ∃p1·Σp1=idΣX and Σp0·∃p1·Σp0= Σp1·∃p1·Σp0 |
cf. Lemma 3.3. They make Q a Σ-split coequaliser.
First, ∃p1·Σp1 =∃p1·∃i·Σi·Σp1 takes φ to (λ y.∃ x.φ(y)∧δ(x,y))=λ y.φ(y) by Remark 8.7 and reflexivity.
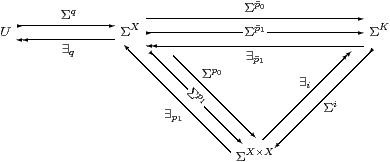
For the other equation, that the two composites Σp0/1·∃p1·Σp0 (for 0 and 1) are equal, it suffices to post-compose the mono ∃i and show that
| ∃i·Σi· Σp0/1·∃p1· ∃i·Σi·Σp0 |
are equal. By Remark 8.7, these composites take φ∈ΣX to
| λ x y.δ(x,y)∧∃ z.(δ(x,z)∧φ(z)) and λ x y.δ(x,y)∧∃ z.(δ(y,z)∧φ(z)) |
respectively. These are indeed equal, by symmetry, transitivity and the Frobenius law.
Since U is defined to split the idempotent ∃p1·Σp0, we have ∃q·Σq=idU, and Σq is a homomorphism by Beck’s theorem. Hence
| Σq·∃q=∃p1·Σp0 =∃p1·∃i·Σi·Σp0, |
which takes φ∈ΣX to
| λ x.∃ y.δ(x,y)∧φ(y) |
by Remark 8.7. Hence φ⊑Σq∃qφ by reflexivity, so ∃q⊣Σq.
For the Frobenius law, again it suffices to apply the mono Σq, which preserves ∧. Let ω∈ΣQ, and put ψ≡ Σqω, so ω=∃qΣqω=∃qψ and ψ=Σq∃qψ. Then
|
are the same by symmetry and transitivity. ▫
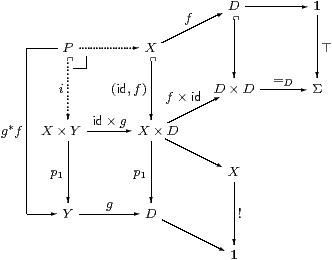
Lemma 10.9 Q is discrete and effective.
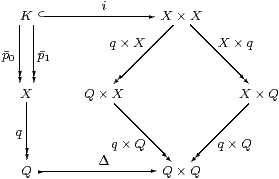
Proof The diagram commutes by manipulation of products and because q∘p0=q∘p1. We have just shown that q is pre-open, whence so are q× X etc. by Proposition 8.2, whilst i is pre-open by hypothesis. So the composite K→ Q× Q is pre-open, but K↠ Q is Σ-epi, so Δ is also pre-open by Lemma 7.2, i.e. ∃Δ⊣ΣΔ satisfies Frobenius. Hence the split mono Δ is the inclusion of an open subset by Theorem 3.10, i.e. Q is discrete. Using surjectivity of K↠ Q,
| ∃Δ·ΣΔ= ∃Δ·∃q∘ p0·Σq∘ p0 ·ΣΔ= ∃q× q·∃i·Σi·Σq× q= ∃q× q(δ∧Σq× q(−))= ∃q× q(δ)∧(−) |
by Frobenius for ∃q× q, so the characteristic map of Δ is (=Q)≡∃q× q(δ).
Then Σq× q(=Q)≡δ since q× q is surjective, i.e. q x=Q q y ⇔ δ(x,y), which says that the quotient is effective. ▫
Theorem 10.10 The full subcategory of overt discrete objects is effective regular,
and is a pretopos if Σ is a distributive lattice.
Proof
Corollary 10.11 Every map between overt discrete objects
factorises as an open surjection followed by an open inclusion.
This factorisation is unique up to unique isomorphism and stable under
pullback along arbitrary C-maps.
Proof Given f:X→ Y, form the quotient q:X↠ Q of the kernel pair K⇉ X of f. Then the mediator i:Q→ Y is mono [Tay99, §5.8], and open by Corollary 10.3. ▫
Remark 10.12 Although ΣX isn’t discrete (except in a topos),
Q is also the image factorisation of
∼δ:X→ΣX:
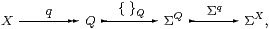
where we check that the composite takes x to λ y.(q x=Q q y), which is λ y.δ(x,y) by effectiveness. The surjection is Σ-split, as are the inclusions, by Proposition 7.12. ▫
This is the traditional construction of the quotient as the set of equivalence classes: an element of Q can be represented either by any element of X that is in the equivalence class or by the characteristic function of this class. The quotient is also constructed using this image factorisation in [Joh77, Proposition 1.23]; see also [BW85, §2.3 Theorem 7].
Peter Freyd and Andre Scedrov [FS90] have shown how to capture the notions of effective regular category and pretopos in terms of relations instead of functions. This approach also transfers attention away from objects and on to the morphisms, so it is possible for there to be “too few” objects for the logic: their condition of tabulation says that all of the objects that the logic describes are actually present. Tabulation plays an analogous role in their theory to the monadicity property in ours, and to the axiom of comprehension in set theory.
See [CW87] for another categorical account of relations.
Proposition 10.13
Assuming only the Euclidean law and not monadicity,
the overt discrete objects of C carry the structure of a (C-enriched)
allegory.
Proof The hom-set Rel(X,Y) is ΣX× Y, which is an internal semilattice. The identity on the discrete object X is (=X) and the composition ΣX× Y×ΣY× Z→ΣX× Z at the overt object Y is defined by
| σ∘ρ = λ x z.∃ y. ρ(x,y)∧ σ(y,z). |
The unit law is that σ(x,z)⇔∃ y.(x=X y)∧ σ(y,z) and associativity follows as usual from the Frobenius law, which itself comes from the Euclidean principle (Theorem 3.10). For the other two Freyd–Scedrov axioms, we have
|
which follow from the Frobenius law and the adjunction ∃Y⊣Σ! by putting y′≡ y and z′≡ z. ▫
Proposition 10.14 If the monadic property also holds then this allegory is
tabular, and is therefore equivalent to the category of relations of
a regular category.
Proof Given a relation ρ:X× Y→Σ, we must find the corresponding open subset U⊂ X× Y. Lemma 3.9 did this. ▫
Remark 10.15 As usual, similar results for compact Hausdorff spaces
follow from the dual Euclidean principle;
in particular they too form a pretopos.
The root of the distinction between the properties of overt discrete and compact Hausdorff spaces is that ℕ is overt, discrete and Hausdorff, but not compact (Remark 7.11). From Corollary 8.4, it follows that all homomorphisms preserve ℕ-indexed joins (but not necessarily meets), whilst ∃f and ∀f, where they exist, preserve joins and meets respectively by virtue of being adjoints.
Remark 10.16 This opens the way to applying the limit–colimit coincidence
from domain theory [Tay87]
to the construction of infinitary colimits of overt discrete spaces
and limits of compact Hausdorff ones.
The following remarks are only intended to sketch the argument,
as the questions of the existence of the relevant limits of algebras in C
and the internal language needed to invoke them
are outside the scope of this paper.
A (filtered) colimit diagram of overt discrete spaces is given by a limit of the corresponding algebras and maps of the form Σf, but this is accompanied by the diagram of the left adjoints ∃f. As all of these maps preserve ℕ-indexed joins, the limit and colimit coincide. Then the limiting cone and colimiting cocone consist respectively of the inverse images and quantifiers for the colimit of the original diagram of overt discrete spaces. In particular, the colimit is overt and discrete. The subcategory also admits initial algebras [E], so it is an arithmetic universe as defined by André Joyal.
Similarly, a (cofiltered) limit diagram of compact Hausdorff spaces gives rise to a filtered colimit of inverse image maps that coincides with the limit of their universal quantifiers. This subcategory also admits final coalgebras.


