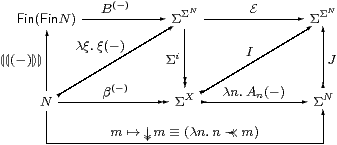



In the next section we shall show that the properties of ≺≺ listed in Section 11 are sufficient to reconstruct the object X and its basis. To do this, however, we need some more technical information about the lattice basis on ΣN, and about the free distributive lattice on N.
Remark 13.1 When an object X has an N-indexed basis (βn,An)
there is an embedding X↣ΣN,
given by Lemma 7.4.
This structure may be summed up by the diagram,

in which {|−|} means the singleton list, the map J on the right is defined by
| Jφ ≡ λξ.∃ n.φ n∧ ξ n, |
and Jφ preserves ∨, ⊥ and ∃. We define E from ≺≺ using the lattice basis (BL,AL) on ΣN.
Remark 13.2
These results may be seen as presentation of the algebra ΣX.
In this, N is the set of generators and
DL(N) is the free (imposed) distributive lattice on them,
which we construct in Proposition 13.8 below.
Then there are homomorphisms
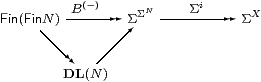
as B(−) takes the imposed list operations 0, 1, + and ⋆ to the intrinsic structure ⊥, ⊤, ∨ and ∧ in ΣΣN, whilst Σi preserves the latter in ΣX. The relation ≺≺ encodes the system of “equations” that distinguishes the particular algebra ΣX from the generic one ΣΣN that is freely generated by N.
This explains why n≺≺ m does not imply n≼ m in our system, whereas α≪β implies α≤β in a continuous lattice. Topologically, we already saw the point in Remarks 1.8 and 6.15: many distinct codes may in principle represent the same open or compact subobject. To put this the other way round, since equality (or containment) of open subobjects is not computable, we cannot deduce equality (or comparison) of codes from semantic coincidence of subobjects.
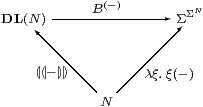
illustrates the comparison between the monad that captures the imposed (0,1,+,⋆) distributive lattice structure and the one in Axiom 3.3 based on Σ(−)⊣Σ(−). The upward maps are the units of these monads. We leave the interested student to construct the multiplication map of the DL-monad as a list program, cf. flatten in Lemma 8.6.
We are not quite justified in saying that the ΣΣ(−) monad defines the intrinsic (⊥,⊤,∨,∧) distributive lattice structure. Corollary 10.3 said that the homomorphisms are the same, but I have not been able to show that every object whose intrinsic order is that of a distributive lattice is an algebra for the monad, i.e. of the form ΣX for some object X.
Notation 13.4 Recall from Proposition 8.8 that the basis on ΣN is
| BL ξ ≡ ∃ℓ∈ L.∀ m∈ℓ.ξ m and AL Φ ≡ ∀ℓ∈ L.Φ(λ m.m∈ℓ), |
from which we obtain the way-below relation
| AL BR ≡ (R⊂♯L) ≡ ∀ℓ∈ L.∃ℓ′∈ R.(ℓ′⊂ℓ). |
The list of lists R+S is given by concatenation, whilst R⋆ S and BR⋆ S were defined in Lemma 8.6.
Lemma 13.5 (BL,AL) is a lattice basis:
| B1=⊤ B0=⊥ BR⋆ S=BR∧ BS BR+S=BR∨ BS |
| A0 Φ⇔⊤ AL⊥⇔(L=0) AR+S=AR∧AS. ▫ |
Lemma 13.6 (BL,AL) is a filter basis:
A⊤⇔⊤ and
AL(Φ∧ Ψ) ⇔ AL Φ ∧ AL Ψ.
Proof
|
The Wilker condition says that we can split the list into the two parts that satisfy the respective disjuncts.
Lemma 13.7 AL(Φ∨ Ψ) ⇔
∃ L1 L2.(L=L1+L2) ∧ AL1 Φ ∧ AL2 Ψ.
▫
Proposition 13.8
We write L≅ R if both R⊂♯L and
L⊂♯R. This is an open congruence for the imposed
structure on Fin(Fin N), and the free imposed distributive lattice
DL(N) is its quotient
(Section C 10). ▫
Remark 13.9 So far we have not used any of the structure on N itself.
Since we have a lattice basis for X, by definition
| β(−): N → ΣX |
takes the imposed structure (0,1,+,⋆) on N to the intrinsic structure (⊥,⊤,∨,∧) on ΣX. Associated with this imposed structure is an imposed order relation ≼, which β(−) takes to ≤, but with respect to which the dual basis A(−) is contravariant.
Definition 13.10 We define ≼ from + and
⋆ as the least relation such that
| 0≼ n≼ n≼1 (k⋆ n)+(k⋆ m) ≼ k*(n+m) |
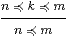

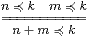
|
and again we write n≅ m when both n≼ m and m≼ n.
Proposition 13.11 The relation ≅ is an open congruence on N whose
quotient is an imposed distributive lattice. ▫
Notation 13.12 Returning to Fin(Fin N), L is regarded as a
formal sum of products of elements of N (additive normal form).
This may be “evaluated” by means of the operation
| ev:Fin(Fin N)→ N. |
This is defined for lists by a generalisation of Lemma 8.6. A similar construction works for Kuratowski-finite subsets instead, except that then N has actually to satisfy the equations for a distributive lattice up to equality, and not just up to ≅ (cf. Notation 4.9). The map
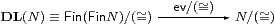
is the structure map of the distributive lattice, regarded as an algebra for the DL-monad.
Proposition 13.13
The map ev:Fin(Fin N)→ N is a homomorphism in the sense that
ev 0=0 and ev 1=1 by construction, whilst
| ev(R+S) ≅ (ev R) + (ev S) and ev(R⋆ S) ≅ (ev R) ⋆ (ev S). |
Proof This is a standard piece of universal algebra, which again we leave as a student exercise. The + equation is proved by list induction, using associativity and commutativity of + up to ≅. The equation for ⋆ is more difficult, as we have to take apart the inner lists, and use distributivity. ▫
|
with equality in the cases L≡{|{|k|}|} and L≡ R.
Proof In the expansion of AL BR, the products in L are of longer strings than those in R. The other three results follow by putting R≡{|{|n|}|}, {|{|n,m|}|} and {|{|n|},{|m|}|}, ▫
Remark 13.15 The foregoing discussion of ≅ is the price that we pay
for not requiring (N,0,1,+,⋆) to satisfy the equations for
a distributive lattice in Remark 1.8.
If, like [JS96], we had done so,
we would have instead paid the same price
to construct the basis for ΣX.
This is indexed by the free distributive lattice
on Nop quâ ⋆-semilattice,
i.e. with new joins but using the old ones as meets.
What we have bought for this price is the flexibility of
switching amongst various kinds of basis (Definition 6.6),
when we needed or didn’t need them, throughout the paper.
The reason why it is unnecessary to form the quotient of N or Fin(Fin N) by the congruence ≅ is that we never deal with their elements up to equality. The things that matter are the rules
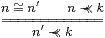
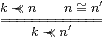
|
which are examples of Corollary 11.5. Indeed the relation ≼ itself is only needed to avoid the extra rules that relate + and ⋆ to ≺≺, which appear in [JS96, Lemma 7].


