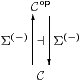


The powerset construction was the force behind set theory as Ernst Zermelo formulated it in 1908, but higher order logic became the poor relation of foundational studies owing to the emphasis on the completeness theorem in model theory. In this paper the powerset plays the leading role, and we derive the first order connectives from it in a novel way. The collection of all subsets is also treated in the same way as the collections of open and recursively enumerable subsets in topology and recursion theory. The underlying formulation in which we do this is a category with a “truth values” object Σ for which the adjunction Σ(−)⊣Σ(−) is monadic. Robert Paré proved in 1974 that any elementary topos has this property, whilst the category LKLoc of locally compact locales has it too (§O 5.10 and Theorem B 3.111). [B] explains how this is an abstraction of Stone duality.
Gerhard Gentzen’s natural deduction was the first principled treatment of the logical connectives, and Per Martin-Löf used the Curry–Howard isomorphism to extend it in a principled way to type constructors [ML84]. However, the natural conclusion of such an approach is to say that the existential quantifier is the same as the dependent sum, i.e. that a proof of ∃ x.φ(x) must always provide a witness: a particular a for which φ(a) holds.
This conflicts with geometrical usage, in which we may say that the Möbius band has two edges, or a complex number two square roots, locally but not globally, i.e. there exists an isomorphism between 2≡1+1 and the set of edges or roots on some open subspace [Tay99, §2.4]. Similarly, interprovable propositions are, for Martin-Löf’s followers, isomorphic types, not equal ones, and their account of the powerset is a bureaucratic one: a structure within which to record the histories of formation and proof of the proposition–types [op. cit., §9.5].
The way in which category theory defines the powerset is not, perhaps, based so firmly on a logical creed as is Martin-Löf type theory, in that it describes provability rather than proof, but it was at least designed for the intuitions of geometry and symmetry. This notion — the subobject classifier in an elementary topos, which is readily generalised to the classifier Σ for open subsets (the Sierpiński space) and recursively enumerable ones — then obeys the curious equation
| σ∧ F(σ)⇔ σ∧ F(⊤) for all σ∈Σ and F:Σ→Σ, |
which we call the Euclidean principle. The Frobenius law, which is part of the categorical formulation of the (geometrical) existential quantifier and was so called by Bill Lawvere, is an automatic corollary of the Euclidean principle. From this we develop the connectives of first order categorical logic, in particular stable effective quotients of equivalence relations.
Whilst set theory and topology have common historical roots [Hau14], the motivation for a common treatment of the kind that we envisage is Marshall Stone’s dictum that we should “always topologize” mathematical objects, even though they may have been introduced entirely in terms of discrete ideas [Joh82, Introduction]. For example, the automorphisms of the algebraic closure of ℚ form, not an infinite discrete (Galois) group, but a compact topological group. Similarly, the powerset of even a discrete set is not itself a discrete set, but a non-Hausdorff topological lattice. (Steven Vickers has taken the same motivation in a different direction [Vic98].)
The types in our logic are therefore to be spaces. The topological structure is an indissoluble part of what it is to be a space: it is not a set of points together with a topology, any more than chipboard (which is made of sawdust and glue) is wood.
When we bring (not necessarily Martin-Löf) type theory together with categorical logic [Tay99], logical notions such as the quantifiers acquire meanings in categories other than Set. In particular, with the internal lattice ΣX in place of the powerset of X, the internal adjunctions ∃X⊣Σ!⊣∀X, where they exist, suggest interpretations of the quantifiers. We shall find that they obey the usual logical rules, but in the topological setting they also say that the space X is respectively overt (a word that we propose to replace one of the meanings of open) or compact.
It is well known that the recursively enumerable subsets of ℕ almost form a topology, since we may form finite intersections and certain infinitary unions of “open” subsets. However, the unification of topology with recursion theory, i.e. making precise Dana Scott’s thesis that continuity approximates the notion of computability, involves a revolutionary change, because the classical axiomatisation of (the frame of open subsets of) a topological space demands that we may form arbitrary unions.
The usual procedure for turning a base (something, like this “topology” on ℕ, that partially satisfies the axioms for a topological space) into a topology would make every subset of ℕ open, losing all recursive information. In particular, in topology an open subspace is glued to its closed complement by means of a comma square construction that is due to Michael Artin, but this doesn’t work for recursively enumerable subsets and their complements [D, Section 4].
Although they are in many respects more constructive, the modern re-axiomatisations of topology in terms of open subsets — the theory of frames or locales [Joh82] that came out of topos theory [Joh77], and Giovanni Sambin’s formal topology [Sam87] motivated by Martin-Löf type theory — have exactly the same fault as Bourbaki’s [Bou66].
The finite meets and joins in the theory of frames present no problem, so what we need is a new way of handling the “purely infinitary” directed joins. Here we use an idea to which Scott’s name has become firmly attached (though it goes back to the Rice–Shapiro and Myhill–Shepherdson theorems of 1955), that directed joins define a topology. However, we turn this idea on its head: by treating frames, not as infinitary algebras over Set, but as finitary ones over Sp (i.e. as topological lattices, cf. topological groups) we can use topology in place of the troublesome directed joins, whenever they are genuinely needed. (Nevertheless, substantial re-working of general topology is needed to eliminate the use of interiors, Heyting implication, direct images, nuclei and injectivity.)
We do this by postulating that, for the category C of spaces, the adjunction
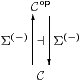
be monadic, i.e. Cop is equivalent to the category of Eilenberg–Moore algebras and homomorphisms over C. In practice, this is used in the form of Jon Beck’s theorem about U-split coequalisers. The way in which this expresses both Stone duality and the axiom of comprehension is explored in Sections B 1 and B 8. The concrete topological model of this situation is the category of locally compact spaces (or locales) and continuous maps.
But this category does not have all equalisers, pullbacks and coequalisers. The impact of this on logic is that we must also reconsider the notions of equality and inequality, which we define by saying that the diagonal subspace is respectively open or closed, i.e. that the space is discrete or Hausdorff.
[It will emerge later in the ASD programme that we cannot, after all, do without equalisers and pullbacks, especially when we consider recursion in [E, Section 2].]
Computational considerations also urge such a point of view. Two data structures may represent the same thing in some ethereal mathematical sense, for example in that they encode functions that produce the same result for every possible input value. However, as we are unable to test them against every input, such an equality may be outside our mortal grasp. A similar argument applies to inequality or distinguishing between the two data structures, in particular real numbers. Equality and inequality, therefore, are additional structure that a space may or may not possess.
Now that equality is no longer to be taken for granted as has traditionally been done in pure mathematics, there are repercussions for category theory. Specifically, Peter Freyd’s unification of products, kernels and projective limits into the single notion of limit in a category [Fre66b] breaks down, because the non-discrete types of diagram depend on equality. This entails a root-and-branch revision of categorical logic, which has traditionally relied very heavily on the universal availability of pullbacks. In fact, most of this work has already been done in categorical type theory [Tay99, Chapters VIII and IX].
The duality between equality and inequality (which also relates conjunction to disjunction and universal to existential quantification) is the characteristic feature of classical logic: for all its other merits, intuitionistic logic loses it. However, we find that it reappears in topology and recursion: for everything that we have to say in this paper about conjunction, equality, existential quantification, open subsets and overt spaces, we find exactly analogous results for disjunction, inequality, universal quantification, closed sets and compact spaces.
This symmetry is a constructive theorem (for LKLoc): as a result of Scott continuity, the Euclidean principle implies its lattice dual. Together with monotonicity (the finitary part of Scott continuity), the two Euclidean principles amount to the Phoa2 principle that has arisen in synthetic domain theory [Pho90a, Hyl91, Tay91]. These are also theorems in the free model of the other axioms. In view of their novelty and unusual form, connections to the Markov principle and several other things have deliberately been left as loose ends.
Whilst Scott continuity is obviously an important motivating principle, the Phoa principle alone has been enough to develop quite a lot of general topology, keeping the open–closed symmetry a precise one so far.
In particular we have a completely symmetrical treatment of open and proper maps, including the dual Frobenius law identified by Japie Vermeulen. Currently it only deals with inclusions and product projections, but the analogue and lattice dual of André Joyal and Myles Tierney’s “linear algebra” for locales [JT84] will be developed in future work.
The topics in general topology that we discuss in the body of the paper converge on a treatment of overt discrete spaces (classically, these are sets with the discrete topology), showing that they form a pretopos. That is, they admit cartesian products, disjoint unions, quotients of equivalence relations and relational algebra. [Assuming Scott continuity, they also admit free monoids and so form an arithmetic universe [E].]
The whole of the paper therefore concerns the logic of the category of sets, even though much of it is written in topological language: what we say about the subcategory of overt discrete spaces is immediately applicable to the whole category when this is Set or an elementary topos. In this sense, we have a new account of some of the early work on elementary toposes, in particular that they satisfy Jean Giraud’s axioms, i.e. that any topos is also what we now call a pretopos.
The distinction between topology and set theory turns out, therefore, to be measured by the strength of the quantifiers that they admit. The paper concludes with a new characterisation of elementary toposes that is based, like Paré’s theorem, on monadicity of the contravariant powerset, but which makes no reference whatever to subsets.

