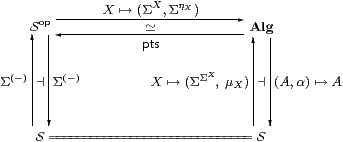



Now we relate subspaces as we have just described them to Stone duality as presented in Section 1. In the abstract setting, the diagrams shown there are as follows, where Alg is the category of Eilenberg–Moore algebras for the monad induced by the adjunction Σ(−)⊣Σ(−).
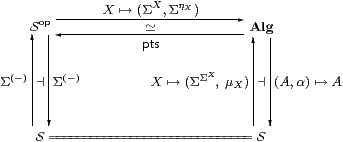
We shall show that subspaces (i.e. certain equalisers) exist in S and carry the subspace topology iff (idempotents split and) the functor Sop→Alg is an equivalence of categories. This functor is full and faithful iff all objects are sober (Theorem A 4.10), so our task in this paper is to say when it is essentially surjective. In fact we shall construct the pseudo-inverse functor. The argument works though the proof of Beck’s theorem in our special case.
Definition 3.1
An algebra (A,α) is spatial if
there is some algebra isomorphism
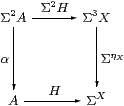
Recall from Lemma A 4.3 that a map H:A→ΣU (not necessarily an isomorphism) is a homomorphism iff its double exponential transpose P has equal composites
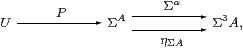
so our first attempt at spatiality of (A,α) is to form this equaliser [Fak70]. Afterwards we have to find out when H is an isomorphism.
Proposition 3.2
The contravariant functor X↦(ΣX,ΣηX):Sop→Alg
has a symmetric adjoint on the right, called pts, so
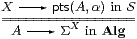
|
iff for each algebra (A,α) the equaliser
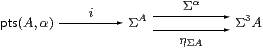
exists in S.
Proof By the foregoing argument, there must also be a correspondence with maps
but this is just the universal property of the equaliser. ▫
The inverse functor pts:Alg→Sop takes the algebra A to the “set” Alg(A,Σ) of homomorphisms, just as the forward one took the object X to the function-space S(X,Σ). (Remark 7.4 explains how Alg(A,B) can sometimes be defined as an object of S, rather than as an external hom-set.)
Theorem 3.3
The contravariant adjunction of
Σ(−) and pts is an equivalence between Sop and
Alg iff all objects of S are sober and all algebras in Alg
are spatial.
Proof Sobriety and spatiality merely say that the units of the symmetric adjunction,
| X→pts(ΣX,ΣηX) and H:A→Σpts A, |
are isomorphisms. ▫
More particularly, without assuming that all objects are sober, the functor pts:Algop→S is full and faithful (making Algop reflective in S) iff all algebras are spatial. Joachim Lambek and Basil Rattray considered this situation abstractly (writing Q A for our Σpts A), together with applications to Abelian categories and elementary toposes [LR75]. More recently, Giuseppe Rosolini connected their results with topos models of synthetic domain theory [BR98a].
We can characterise spatiality in terms more like those of the previous section.
Proposition 3.4
(A,α)≅ΣX iff
there are i:X→ΣA and I:ΣX→Σ2 A such that
| i is prime, I;Σi=idΣX and Σi;I=α;ηA≡ηΣ2 A;Σ2α. |
In this case, i:X=pts(A,α)→ΣA is the equaliser in Proposition 3.2, and Σ(−) takes it to a split coequaliser.
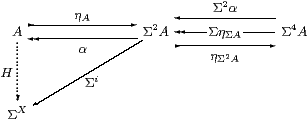
Proof If H:A≅ΣX is an isomorphism of algebras then its double exponential transpose i ≡ ηX;ΣH is prime, and we may put I ≡ H−1;ηA=ηΣX;Σ2 H−1. Then
| I;Σi = ηΣX;Σ2 H−1;Σ2 H;ΣηX = ηΣX;ΣηX = id |
| Σi;I = Σ2 H;ΣηX;H−1;ηA = α; H;H−1;ηA = α; ηA. |
Conversely, if i is prime then its double transpose H≡ηA;Σi is a homomorphism, and H−1=I;α because
| ηA;Σi;I;α = ηA;α;ηA;α = id |
| I;α;ηA;Σi = I;ηΣ2 A;Σ2α;Σi = I;ηΣ2 A;ΣηΣA;Σi = I;Σi = id |
since i, being prime, has equal composes with Σα and ηΣA.
To show that X is the equaliser, consider P:Γ→ΣA⇉Σ3 A. The double transpose K:A≡ΣX→ΣΓ of P is a homomorphism, so, since X is sober, K=Σk, where k:Γ→ X mediates to the equaliser. The image of the equaliser diagram under Σ(−) is the split coequaliser shown above. ▫
Remark 3.5 In the λ-calculus, these equations are
|
The η-equation, which says that ΣX is a retract of A, was discussed in the previous section: it makes X a Σ-split subspace of ΣA.
The β-equation makes H:A↣ΣX a subalgebra that is “U-split” in Beck’s language, i.e. split by a function that need not be a homomorphism. This property says that there are enough points to distinguish the elements of A, considered as “open subsets” of X.
Remark 3.6 The same caveat applies to our definition of “spatial” algebras
as to that of “sober” spaces in
Remark A 5.10:
the correspondence with the lattice-theoretic notion in
[Joh82, Section II 1.5]
is a conceptual one rather than a theorem.
In particular, recall from [Joh82, Theorem VII 4.3] that
(using the axiom of choice) any distributive continuous lattice A
has enough points (completely coprime filters) in the classical sense.
All algebras over LKLoc are spatial in the constructive sense that
there are enough generalised “points”
Γ→pts(A,α), cf. [Vic95].
Beck’s theorem and our treatment of subspaces consider the maps and equations in the main equaliser diagram, without requiring the objects to be Σ2 A, Σ3 X, etc.
Definition 3.7
A parallel pair u,v:Y⇉ Z in S
is called a Σ-split pair
if there is some map (not necessarily a homomorphism) J:ΣY→ΣZ
such that
| J;Σu = idΣY and Σu;J;Σv = Σv;J;Σv. |
Notice that we just mark one of the maps with a hook, to emphasise the fact that the conditions are not symmetrical in u and v.
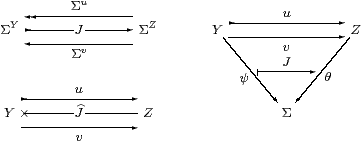
It is helpful to see these equations expressed in other ways. Using Notation 2.11, they are
| u; |
| = id and v; |
| ;u = v; |
| ;v. |
Mixing application with categorical composition, we have
| u;J(ψ) = ψ and v;J(u;θ) = v;J(v;θ). |
Using the λ-calculus, the equations are
|
We shall need the equaliser i:X→ Y of u and v, for which we would like Σi:ΣY→ΣX also to be the coequaliser of Σu and Σv. In this case there is a (unique) map I:ΣX→ΣY with I;Σi=idΣX and Σi;I=J;Σv.
Reversing the arrows, there is a similar notion of Σ-split coequaliser (Section 11), whilst (unqualified) split equalisers and coequalisers also arise, in which the equations already hold at the base level, without applying the functor Σ(−). Split (co)equalisers are absolute in the sense that, being equationally defined, they are preserved by all functors. Absolute coequalisers were first studied by Robert Paré [Par71]. Examples of absolute pushouts may be found in Section 7, [Tay99, Exercise 5.3] and [D].
We construct the equaliser of a split pair by splitting an idempotent (Remark 4.1). In particular, ΣX splits E ≡ Σv;J. Conversely, any idempotent e:Y→ Y gives rise to a split pair (e,id), with J ≡ E ≡ Σe, so such splittings are necessary.
There is no greater generality in supposing that i is split only after further iteration of the functor Σ(−), since if I;Σ3 i=id then I;Σi=id by the unit law, where I ≡ ηΣX;I;ΣηY.
Proposition 3.8
If the functor pts exists,
all objects are sober and idempotents split, then
S has equalisers of all Σ-split pairs.
If, additionally, all algebras are spatial,
Σ(−) takes these equalisers to (split) coequalisers.
Conversely, if S has equalisers of all Σ-split pairs, and Σ(−) takes them to coequalisers, then all algebras are spatial.
Proof Let u,v:Y⇉ Z have splitting J:ΣZ→ΣY, so that E ≡ Σv;J is an idempotent on ΣY, and let A be its splitting, as in the top rows of the diagrams. Since this coequaliser is absolute, Σ2 A is also a coequaliser, so the structure α may be obtained as the mediator; similar arguments involving Σ4A show that it satisfies the equations for an Eilenberg–Moore algebra.
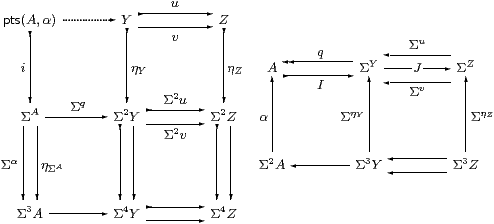
I claim that pts(A,α) is the equaliser of u and v.
All composites pts(A,α)→Σ4 Y are equal, so they factor through ηY since Y is sober. This defines the dotted map. It has equal composites with u and v because all composites pts(A,α)→Σ2 Z are equal and ηZ is mono.
Any test map Γ→ Y having equal composites with u and v also has equal composites with Σ2 u and Σ2 v, since η is natural, so it factors through their equaliser, ΣA. For the same reasons it has equal composites with ΣA⇉Σ3 A, and so factors through their equaliser pts(A,α). The mediator is unique because i and Σq are mono.
Now apply Σ(−) to the left-hand diagram, so Σpts(A,α)≅ A and Σi≅α by Theorem 3.3 since A is spatial. Then Σ(−) takes the top two rows of the diagram on the left to the one on the right.
Since pts is itself a Σ-split equaliser, the converse follows from Proposition 3.4. ▫
Remark 3.9 Because of the fact that Σ(−) takes it
to the coequaliser of ΣY⇇ΣZ,
the diagram X→ Y⇉ Z is also an equaliser in HS,
i.e. with respect to “second class” test maps
F:Γ−× Y⇉ Z (Notation 2.11).
This is in contrast to the situation for products, where the failure of the extension of the universal property from S to HS is essentially related to the interpretation of computational effects [Thi97a]. The fact that equalisers are valid even in the presence of such effects may be regarded as the categorical justification of the use of Floyd–Hoare logic for imperative as well as functional programs.
It is still not clear precisely what the exactness properties of Σ(−) should be, as not all equalisers are taken to coequalisers:
Example 3.10 (Steven Vickers) Suppose that S has disjoint coproducts,
as is the case for Set and LKSp,
and also in the abstract situation by Theorem 11.8.
Then
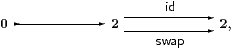
is an equaliser (where swap interchanges the elements of 2), but Σ(−) takes it to
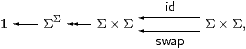
where swap interchanges the components of the product. ▫
We can now prove the intuitionistic form of Stone duality for locally compact locales.
Theorem 3.11
LKLoc is monadic.
Proof We must show that every object is sober, that equalisers of Σ-split pairs exist, and that Σ(−) takes them to coequalisers. Recall from the theory of locales and continuous lattices [GHK++80, Joh82] that the topology on a locally compact locale is a distributive continuous lattice, whilst the category Cont of continuous lattices and Scott continuous functions is fully embedded (via the Scott topology) as a subcategory of LKLoc that is closed under retracts.
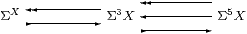
The equaliser diagram of locales involved in the definition of sobriety gives rise to diagram of frames shown above, where ↞ denotes a frame homomorphism and ↣ a Scott continuous function. This is a split coequaliser in Cont and so ā fortiori a coequaliser in LKFrm, i.e. an equaliser in LKLoc.
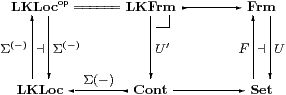
Now let u,v:Y⇉ Z be a Σ-split pair in LKLoc. We follow it around the diagram of categories and functors above.
E ≡ J;Σv is a Scott continuous idempotent on the continuous frame ΣY, so it is split by some continuous lattice Q. Hence
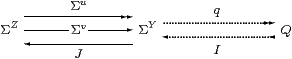
is a split coequaliser diagram in LKLoc, although we may just as well see it as being in Cont or Set.
The forgetful functor U:Frm→Set, being monadic [Joh82, Theorem II 1.2], creates this coequaliser in Frm, so the lattice Q is actually a frame, and the map ΣY↠ Q is a frame homomorphism. This means that Q≅ΣX for some locale X, which is locally compact since Q is continuous, and q ≡ Σi. Hence the diagram is a coequaliser in LKFrm, so X is the equaliser in LKLoc, which Σ(−) takes to the original split coequaliser. ▫
We conclude our introductory discussion with an example of a non-spatial algebra.
Classically, the two-point set classifies subsets in Set, open subsets in LKSp (when it is given the Sierpiński topology), and upper subsets in Pos (when it is given the order ⊥<⊤). The monad may therefore be defined on Pos using this object, which we call Υ.
Example 3.12 In (Pos,Υ), all objects are
sober classically but not intuitionistically
(Remark C 5.10(c)). Pos does not have the monadic
property, because the unit interval, A=[0,1] with the usual
arithmetical order, is an Eilenberg–Moore algebra (in a unique way)
that does not have enough points.
This discussion of [0,1] extends that in [FW90, Example 9]. In fact, the algebras for this version of the monad are constructively completely distributive lattices [MRW02].
Proof Classically, the upper sets of A are of the form (a,1] or [a,1]. Indeed ΣA· n=Aop·(n+1), where A· n is A×n with the lexicographic order: <a,i>≤<b,j> if a< b, or a=b and i≤ j.

The maps we’re interested in act as the identity on the real part, and as shown above on the numerical part. ▫


