


We still have to show that SC has powers of Σ, and that all of its objects are sober. In fact SC freely adjoins sobriety to C.
Lemma 7.1
Still writing Σ(−) for the exponential in C,
SC(X,ΣY)≅ C(X,ΣY),
where the homomorphism H:Σ2 Y→ΣX
corresponds to the map f:X→ΣY by
| H=Σf and f=ηX;ΣH;ΣηY. |
Proof H∈SC(X,ΣY) is by definition a homomorphism H:Σ2 Y→ΣX, whose double exponential transpose P:X→Σ3 Y has equal composites with Σ3 Y⇉Σ5 Y by Lemma 4.3, and so factors as f:X→ΣY through the equaliser by Proposition 4.9. More explicitly,
| ηX;ΣΣf;ΣηY = f;ηΣY;ΣηY = f |
by Lemma 2.10, and
| Σf = ΣΣηY;ΣΣH;ΣηX = ΣΣηY;ΣηΣY;H = H |
since H is a homomorphism. ▫
Proposition 6.11 (and the way in which objects of SC are named) allow us to use the product notation ambiguously in both categories. Relying on that, we can now also justify writing ΣX for powers in either C or SC.
Corollary 7.2 SC has powers of Σ and
C→SC preserves them.
Proof SC(Γ×SC X,Σ) = SC(Γ×CX,Σ) by Proposition 6.11. Then by the Lemma this is C(Γ× X,Σ) ≅ C(Γ,ΣX)≅SC(Γ,ΣX). ▫
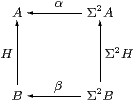
Proof AlgSC is defined from SC in the same way as AlgC≡Alg is defined from C (Definition 3.2). Consider the defining square for a homomorphism over SC:

The vertices are retracts of powers of Σ, and Lemma 7.1 extends to such objects. Hence the SC-maps α, β and H might as well just be C-maps, by Lemma 7.1, and the equations hold in SC iff they hold in C. ▫
Proposition 7.4 All objects of SC are sober,
SSC≅SC and HSC≅HC.
Proof The categories all share the same objects, and by Lemma 7.1,
| HSC(X,Y) = SC(ΣY,ΣX) ≅ C(ΣY,ΣX) = HC(X,Y). |
Lemma 7.3 provides the analogous result for SC, namely
| SSC(X,Y) = AlgSC(ΣY,ΣX) ≅ Alg(ΣY,ΣX) = SC(X,Y). |
Then all objects of SC are sober by Theorem 4.10. ▫
By Corollary 4.12, SC therefore has focusP for every prime P. The construction in the previous section shows that this is given by composition with the second class map force.
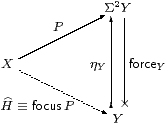
Proof The correspondence between H and P is double exponential transposition (Proposition 2.11), and H is a homomorphism (i.e. H is in SC) iff P is prime, by Lemma 4.3. In particular, H=idΣX corresponds to P=ηX. When H is a homomorphism we have
| P = ηX;ΣH = ηX;Σ2 |
| = |
| ;ηY, |
or thunk(a), where x:X⊢ a:Y is the term corresponding to H, so
| focusP = focus(thunka) = a. ▫ |
Theorem 7.6 SC is, up to isomorphism,
the universal way of forcing all objects of C to be sober.
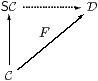
Proof Let D be a category with products and an exponentiating object ΣD, and let F:C→D be a functor that preserves this structure. Suppose that all objects of D are sober. Given any homomorphism H:ΣY→ΣX in C, consider its image under the functor in D. This is a homomorphism F H:ΣDF Y→ΣDF X since F commutes with Σ(−) and preserves the Eilenberg–Moore equation. Therefore F H is of the form ΣDg for some unique g:F X→ F Y, since all objects of D are sober. Then g is the effect of F on the given SC-morphism H:X→ Y.
This construction preserves identities and compositions by the usual uniqueness arguments, and similarly if H=Σf with f:X→ Y in C then g=F f. Hence we have a commutative triangle of functors. As the objects X and Y of SC are just objects of C and F(X× Y)≅ F X× F Y on C, products in SC are also preserved, as are powers of Σ. ▫
Remark 7.7 Peter Selinger, for whom (his version of) the computational
category HC is of primary interest,
calls C and SC value categories,
and takes an egalitarian view of them [Sel01, Section 3.5].
However, we have just shown that SC has a universal property,
so it is the sober completion of C,
and such (established) language does make a value-judgement:
we regard SC as better than C,
since it includes denotational values that we have argued ought
to be present.
Be careful, however, to distinguish this sober completion of the category C from the sobrification X of the space (object) X [Joh82, Corollary II 1.7(ii)]. If C has equalisers, X is obtained by forming the equaliser that we used to define sobriety (cf. Remark 4.8). In [B] we shall obtain the space pts(A,α) of points of an arbitrary algebra by forming an equaliser of this kind. These “concrete” constructions on objects are carried out within a single sufficiently expressive category, whereas SC is a new category that is obtained “abstractly” by re-naming features of the old category C.
Remark 7.8 What of the extra structure in Remarks 2.4ff?
The lattice operations ⊤, ⊥, ∧ and ∨, being
morphisms 1→Σ or Σ×Σ→Σ in C,
are carried by the functor C→SC into the new category.
The equations for a distributive lattice still hold,
because any functor preserves equations, and this one also preserves products.
The Euclidean principle remains valid in the new category too,
as ΣΣ is also preserved.
This leaves ℕ, from which preservation of the existential quantifier and
continuity axiom follow easily.
The only issue is in fact the way in which new values are created in SC by the combination of focus and primitive recursion. We leave the reader to add parameters: S:Γ×ℕ× X→ X.
Proposition 7.9 C→SC preserves the natural numbers object,
i.e. ℕ admits primitive recursion in SC.
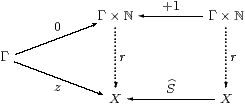
Proof The recursion data consist of z:Γ→ X and a homomorphism S:ΣX→ΣX. So Z≡ z;ηX is prime and has equal composites in the lower triangle below, whilst the parallel squares each commute, by naturality of η.
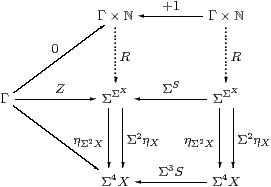
As ℕ has the universal property in C, there are mediators R:Γ×ℕ→Σ2 X and Γ×ℕ→Σ4 X making the whole diagram commute. But, by uniqueness of the second, the composites Γ×ℕ⇉Σ4 X are equal, so R is prime by Lemma 4.3, and focusR:ℕ→ X is the required mediator in SC. ▫
Finally, we note a result that would hold automatically if SC were a cartesian closed category.
Lemma 7.10 The functor SC→Cop preserves such colimits as exist.
Proof The diagram for a colimit in SC is a diagram for a limit in C whose vertices are powers of Σ and whose edges are homomorphisms. If the diagram has a colimit C in SC then it is a cone of homomorphisms in C with vertex ΣC whose limiting property is tested by other cones of homomorphisms from powers of Σ. We have to extend this property to cones from arbitrary objects Γ of C.
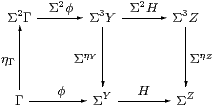
Let φ:Γ→ΣY be a typical edge of the cone and H:ΣY→ΣZ an edge of the diagram. Then Σ2φ;ΣηY:Σ2Γ→ΣY is a homomorphism, and is an edge of a cone with vertex Σ2Γ because the diagram above commutes.
Hence there is a mediator Γ→Σ2Γ→ΣC to the limit. It is unique because any other such mediator Γ→ΣC can be lifted to a homomorphism Σ2Γ→ΣC in the same way, and this must agree with the mediator that we have. ▫
Proposition 7.11
The functor X×(−) preserves (distributes over)
such colimits as exist in SC.
Proof The functor X×(−) on SC is (−)X on C, which is defined at powers of Σ and homomorphisms between them. If C is the colimit of a diagram with typical edge H:Z→ Y in SC then the Lemma says that ΣC is the limit of the diagram with typical edge H:ΣY→ΣZ in C. Now (−)X, in so far as it is defined, preserves limits, since it has a left adjoint X×(−) in C. (You may like to draw the diagrams to show this explicitly.) Hence ΣC× X is the limit of the diagram with typical edge HX:ΣX× Y→ΣX× Z in C. Since fewer (co)cones have to be tested, C× X is the colimit of the diagram with typical edge X×H:X× Y→ X× Z in SC. ▫


