11  The way-below relation

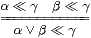
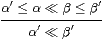
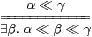
We now introduce the last (g) of our abstract characterisations of local compactness in the Introduction. Recall from Section 2 that any continuous distributive lattice carries a binary relation (written ≪ and called “way-below”) such that

⊥≪γ

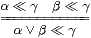
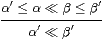
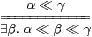
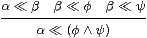
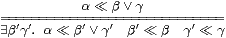
Notation 11.1 We define a new relation n≺≺ m as A_nβ^m.

This is an open binary relation (term of type Σ with two free variables) on the overt discrete object N of indices of a basis, not on the lattice Σ^X. It is an “imposed” structure on N in the sense of Remark 4.5.

For most of the results of this section, we shall require (βⁿ,A_n) to be an ∨-basis for X.

Examples 11.2 (Not all of these are ∨-bases.)

1. Let βⁿ classify Uⁿ⊂ X, and A_n=λφ.(Kⁿ⊂φ) in a locally compact sober space. Then n≺≺ m means that Kⁿ⊂ U^m. This is consistent with Notation 1.3 if we identify the basis element n with the pair (Uⁿ⊂ Kⁿ).
2. Let A_n=λφ.(βⁿ≪φ) in a continuous lattice. Then n≺≺ m means that βⁿ≪β^m, cf. Definition 2.3.
3. In the interval basis on ℝ in Example 6.10, <q,δ>≺≺<p,є> means that [q,δ]⊂(p,є), i.e. p−є< q−δ≤ q+δ< p+є.
4. In the basis of disjoint pairs of opens, (Uⁿ⋔ V_n), for a compact Hausdorff space in Example 6.11, n≺≺ m means that V_n∪ U^m=X.
5. In the prime basis ({n},η n) for N in Example 1, n≺≺ m just when n=m.
6. In the Fin(N)-indexed filter ∨-basis on N in Proposition 8.8, ℓ≺≺ℓ′ iff ℓ⊂ℓ′.
7. In the prime ∧-basis on Σ^N in Example 2, on the other hand, ℓ≺≺ℓ′ iff ℓ′⊂ℓ.
8. More generally, in the prime ∧-basis on Σ^X derived from an ∨-basis on X in Lemma 9.8, (n≺≺_Σ^Xm) iff (m≺≺_X n).
9. In the Fin(Fin(N))-indexed filter lattice basis on Σ^N in Proposition 8.8,

   L≺≺ R  ≡  AL BR  ⇔  R⊂♯L  ≡  ∀ℓ∈ L.∃ℓ′∈ R.(ℓ′⊂ℓ),

   where R⊂^♯L is known as the upper order on subsets induced by the relation ⊂ on elements.
10. In the prime ∧-basis on Σ^ΣN in Lemma 8.9, L≺≺ R iff L⊂^♯R.
11. In the ∨-basis on Σ^ΣX derived from an ∨-basis on X in Lemma 9.9,

    (ℓ≺≺Σ2 Xℓ′)  ⇔ (ℓ≺≺X♯ℓ′).

12. Any stably locally compact object X has a filter lattice basis (N,0,1,+,⋆,≺≺) such that the opposite (N,1,0,⋆,+,≻≻) is the basis of another such object, known as its Lawson dual (Proposition 12.14).

Our first result just restates the assumption of an ∨-basis, cf. Lemmas 1.9 and 2.6:

Lemma 11.3 0≺≺ p, whilst n+m≺≺ p iff both n≺≺ p and m≺≺ p.

Proof    A₀β^p⇔⊤ and A_n+mβ^p⇔ A_nβ^p∧ A_mβ^p.         ▫

In a continuous lattice, α≪β implies α≤β, but we have no similar property relating ≺≺ to ≼. We shall see the reasons for this in Section 13. But we do have two properties that carry most of the force of α≪β⇒α≤β. We call them roundedness. The second also incorporates many of the uses of directed joins and Scott continuity into a notation that will become increasingly more like discrete mathematics than it resembles the technology of traditional topology.

Lemma 11.4 βⁿ=∃ m.(m≺≺ n)∧β^m and A_m=∃ n.A_n∧(m≺≺ n).

Proof    The first is simply the basis expansion of βⁿ. For the second, we apply A_m to the basis expansion of φ, so

since A_n preserves directed joins (Theorem 9.6).         ▫

Corollary 11.5 If m≺≺ n then β^m≤βⁿ and A_m≥ A_n.         ▫

Corollary 11.6 If m≺≺ n, A_m′≥ A_m and βⁿ≤β^n′, then m′≺≺ n′.

Proof    (m≺≺ n)≡ A_mβⁿ⇒ A_m′β^n′≡(m′≺≺ n′).         ▫

Corollary 11.7 The relation ≺≺ satisfies transitivity and the interpolation lemma:

Proof    A_mβⁿ ⇔ (∃ k.A_k∧ m≺≺ k)βⁿ ⇔ ∃ k.A_kβⁿ∧ m≺≺ k.         ▫

Now we consider the interaction between ≺≺ and the lattice structures (⊤,⊥,∧,∨) and (1,0,+,⋆). Of course, for this we need a lattice basis.

Lemma 11.8 As directed joins,

Proof    The first is the Frobenius law, since β^{p⋆ q}=β^p∧β^q.

The second uses Lemma 4.17: we obtain the expression

from the basis expansion φ=∃ p.A_pφ∧β^p by adding ψ to the 0th term (since A₀φ⇔⊤ and β⁰=⊥) and, harmlessly, A_pφ∧ψ to the other terms. Similarly,

The joins are directed because because A₀φ∧ A₀ψ⇔⊤ and

Lemma 11.9 For a lattice basis, A_n⊤⇔(n≺≺1), A_n⊥⇔(n≺≺0) and

Proof    The first two are A_nβ¹ and A_nβ⁰. The other two are ∃ p q.A_n(β^{p⋆ q})∧ A_pφ∧ A_qψ and ∃ p q.A_n(β^p+q)∧ A_pφ∧ A_qψ, which are A_n applied to the directed joins in Lemma 11.8.         ▫

Proposition 11.10 The lattice basis (βⁿ,A_n) is a filter basis iff 1≺≺1 and

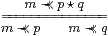
Proof    (n≺≺1)⇔ A_nβ¹⇔ A_n⊤, but recall that n≺≺1 for all n iff 1≺≺1.

The displayed rule is A_mβ^p∧ A_mβ^q ⇔ A_mβ^{p⋆ q} ≡ A_m(β^p∧β^q). Given this, by the Frobenius law and Lemma 11.9,

If we don’t have a filter basis, we have to let n “slip” by n≺≺ m, cf. Lemma 2.8:

Lemma 11.11 For any lattice basis,

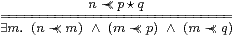
Proof    Downwards, interpolate n≺≺ m≺≺ p⋆ q≼ p,q, then m≺≺ p,q by monotonicity. Conversely, using Corollary 11.5, if A_nβ^m⇔⊤ and β^m≤β^{p⋆ q} then A_nβ^{p⋆ q}⇔⊤.         ▫

The corresponding result for ∨ is our version of the Wilker property, cf. Proposition 1.10 and Lemma 2.7.

Lemma 11.12

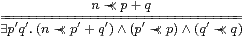
Proof    Lemma 11.9 with φ≡β^p and ψ≡β^q.        ▫

We shall summarise these rules in Definition 14.1.

There are special results that we have in the cases of overt and compact objects. We already know that 1≺≺ 1 iff the object is compact (cf. Lemma 6.5), but the lattice dual characterisation of overtness cannot be 0≺≺ 0, as that always happens.

Lemma 11.13 If X is overt then

Proof    φ x⇒ ∃ y.φ y so, using the Phoa principle (Axiom 3.6),

Putting φ≡β^m,

whilst (n≺≺ 0) ∧ ∃ x.βⁿ x  ⇔  ∃ x.A_nβ⁰∧βⁿ x  ⇒  ∃ x.∃ n.A_n⊥∧βⁿ x  ⇔  ∃ x.⊥ x  ⇔  ⊥.         ▫

By a similar argument, we have Johnstone’s “Townsend–Thoresen Lemma” [Joh84],

Corollary 11.14 Given a compact overt object, it’s decidable whether it’s empty or inhabited, cf. Corollary 5.8.

Proof    As (1≺≺1)⇔⊤, the Lemma makes (1≺≺0) and ∃ x.β¹ x≡∃ x.⊤ complementary.         ▫

Compact overt subobjects are, in fact, particularly well behaved in discrete [E] and Hausdorff [J] objects.

Sections 13–16 are devoted to proving that the rules above for ≺≺ are complete, in the sense that from any abstract basis (N,0,1,+,⋆,≺≺) satisfying them we may recover an object of the category. This proof is very technical, so in the next section we consider a special case, in which the lattice structure plays a much lighter role.