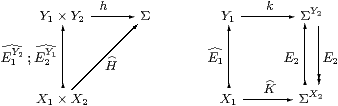



Now that we have overcome the main difficulty concerning binary products, we are equipped to tackle exponentials, and then to show that S does in fact have the monadic property for which it was designed. We still rely on injectivity, first re-casting Proposition 5.2 in terms of the double transpose of h.
Lemma 6.1
There is a natural bijection between S-maps
H:{Y ∣ E}→ΣU and S-maps p:U→ΣY
such that p=p;E.
Proof Let H↦ p=ηU;H, which satisfies p=p;E by Lemma 4.6. Conversely, let p↦H=E;ηY;Σp, which is a composite of S-maps {Y ∣ E}↣ Y→ΣU.
Then H↦ E;ηY;Σp= E;ηY;ΣH;ΣηU= H;ηΣU;ΣηU= H by Definition 4.5 and the unit law. Conversely, p↦ ηU;H=ηU;Σ2 p;ΣηY;E= p;ηΣY;ΣηY;E= p;E=p by naturality for η and the unit law.
For naturality, let F:{Y′ ∣ E′}→{Y ∣ E} and g:U′→ U. Then p becomes g;p;F. ▫
Proposition 6.2
S has and S→S preserves powers of Σ, where
| Σ{Y ∣ E} ≡ {ΣY ∣ ΣE} and Σ |
| ≡ F. |
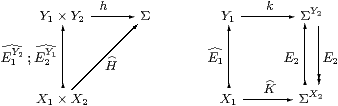
Proof S-maps H:X1× X2→Σ correspond bijectively to p:1→ΣY1× Y2 in S such that p=p;E1Y2;E2Y1, by Lemma 6.1. By Remark 5.10, this is equivalent to p;E1Y2=p=p;E2Y1. Let k:Y1→ΣY2 and q:Y2→ΣY1 be the exponential transposes of p, which satisfy k=k;E2 and q=q;E1. But then q corresponds to K:X1→ΣY2 by Lemma 6.1, and K=K;E2 by the other equation, so it factors through ΣX2. Conversely, K defines k, q, p and H in the same way.
Now let F1:X′1→ X1 and F2:X′2→ X2, whose product is F1X′2;F2X1 by Proposition 5.12. Then by the naturality part of the Lemma, p becomes p;F2X1;F1X′2 and K becomes F1;K;F2. ▫
Lemma 6.3
ηX:X→Σ2 X in S
is given by E;ηY:Y−×Σ2 Y.
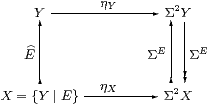
Proof From functoriality in the Proposition, Σ2 takes the inclusion E to ΣE. Then for η to be natural on S, we need ηX=E;ηY;ΣE. But this expression is the left hand side of the defining equation for the nucleus E (Definition 4.3), the right hand side being E;ηY.
Alternatively, we may see η{Y ∣ E} as the double transpose of id{Y ∣ E}≡E. This correspondence is that between k and q on the right hand side of the Proposition, in the case of X1=ΣX, X2=X. Then K=idΣX=E=k and q=ηY;ΣE, so η{Y ∣ E}=E;q=E;ηY. ▫
Corollary 6.4
AlgS≃AlgKSS≅AlgKS, cf. AlgSS≅AlgS in Lemma A 7.3.
Proof Let (A,α) be an algebra over S, with A ≡ {Y ∣ E}. Then A◁Σ2 A◁Σ2 Y, so A may as well be in KS, since this is fully embedded in S by Corollary 4.13. ▫
Lemma 6.5 S-maps H:X1−× X2 are given by
| H:ΣY2→ΣY1 such that H;E1 = H = E2;H. |
So HS⊂KHS is the full subcategory consisting of those objects (X,E) for which E is a nucleus.
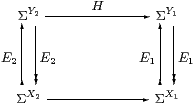
Proof An HS-map H:X1−× X2 is a S-map H:ΣX2→ΣX1. We have just shown that these exponentials are retracts, so this map is H:ΣY2→ΣY1 (now just in S) such that E2;H=H=H;E1. This is also how morphisms of KHS are defined (Remark 4.1). ▫
Lemma 6.6
An HS-map H:X1−× X2 is first class (a S-map)
iff it respects naturality of η,
i.e. ηX1;Σ2H=H;ηX2,
or H:ΣX2→ΣX1 is a homomorphism.
Proof Using the previous two lemmas,
| ηX1;Σ2 |
| = |
| ;ηY1;Σ2 |
| and |
| ;ηX2 = |
| ; |
| ;ηY2 = |
| ;ηY2. |
Equality of these is the second equation in Definition 4.5. ▫
Corollary 6.7
Every homomorphism K:ΣX2→ΣX1 in
S is of the form K=ΣH for some unique
S-map H:X1→ X2.
From Section A 7 we deduce that
all objects of S are sober, that SS≅S and that
X×(−) distributes over such colimits as exist in S. ▫
Notation 6.8
Recall from Definition A 6.3
that we wrote force:Σ2 X−× X for the HS-map
ηΣX, and that this is natural with respect to
HS-maps H:X−× Y.
Similarly, we now write
| admit for |
| : Y −× {Y ∣ E}. |
Like the identity, the inclusion i:(Y⇉ Z)↪ Y and its splitting I are both encoded as E. In Section 8 we shall add an operator admit to the λ-calculus, just as we introduced focus in Section A 8, and they both have side-conditions. However, we shall not on this occasion give different names to the operator in S and the map in HS.
Lemma 6.9
force{Y ∣ E} = Σ2 i ; forceY ; admit.

Hence if Γ⊢ P:Σ2 {Y ∣ E} is prime then so is Γ⊢Σ2 i P:Σ2 Y and
| focus{Y ∣ E} P = admit(focusY(Σ2 i P)). |
Proof The diagram shows naturality of force with respect to admit in HS, i.e. of η with respect to E in S. Recall from Lemma A 4.3 that P is prime iff it has equal composites with Σ2η(−) and ηΣ2(−), which are natural with respect to i:{Y ∣ E}↣ Y. ▫
Now we can show that S has the new structure that it was introduced to provide.
Proposition 6.10
Σ-split equalisers exist in S,
and Σ(−) sends them to coequalisers. Indeed
| {{Y ∣ E1} ∣ E2} = {Y ∣ E2} |
where X ≡ {Y ∣ E1} is a S-object and E2 data on it for a S-object {X ∣ E2}.
Proof The defining equations for E2 to be an HS-map and to be a nucleus (Definition 4.3), i.e. to define an S-object, are
| ; |
| = |
| = |
| ; |
| and |
| ;ηX;ΣE2 = |
| ;ηX, |
the first of which says that E2⊂E1 in the sense of Notation 4.4. The second equation, between HS-maps, reduces to
| ;ηY;ΣE2 = |
| ;ηY |
in HS, but this is just the definition of a nucleus E2 on Y. Hence {Y ∣ E2} as a S-object, which Lemma 4.12 expresses as the equaliser of a Σ-split pair Y⇉Σ2 Y:
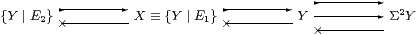
Finally, Σ(−) acts on this diagram in S just as it does in S, taking it to a split coequaliser, as in Proposition 4.14. ▫
Corollary 6.11
(S,Σ) is monadic and S≃AlgKSop.
Proof Recall that being monadic means that S≃AlgSop. By Theorem 3.3, this happens iff all objects are sober (which they are by Corollary 6.7) and all algebras are spatial. The latter follows from the previous result by Proposition 3.8. Finally, the equivalence with AlgKSop is given by Corollary 6.4. ▫
Theorem 6.12
(S,Σ) is the (Karoubi and)
monadic completion of (S,Σ):
Let (D,ΣD) be monadic and suppose that idempotents split in D (so D has products, powers of ΣD, equalisers of ΣD-split pairs and ΣD(−) sends them to coequalisers.) Let F:S→D be a functor that preserves products and powers of Σ. Then there is a functor F:S→D that also preserves these things and makes the square commute, and it is unique up to equivalence.

Proof Any object of S is interpreted as a Σ-split equaliser diagram in S as in Proposition 4.14. Such diagrams are preserved by the functor F, but the diagram in D has an equaliser, which is the required image of the given S-object. F commutes with the representation of × and Σ(−) in Propositions 5.12 and 6.2. ▫
Remark 6.13 The sober, Karoubi and monadic completions are related by the diagram
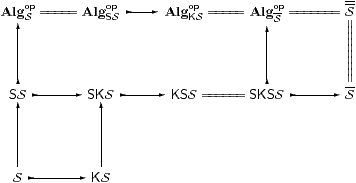
in which ↣ denotes a full inclusion and = an equivalence. We leave the interested reader to find a properly general recursive idempotent on ℕ (so SKS≠KSS, cf. Remark A 9.12), and to show that any retract of a sober object is sober (so KSS=SKSS). ▫
The development so far has been entirely set in the abstract situation of a category S with an exponentiating object Σ, for which all objects are sober. In the intended applications to topology and computation, Σ is a distributive lattice and satisfies the Euclidean principle [C]; this structure is preserved by the inclusion S→S since it preserves products and powers of Σ.
We also want S to have a natural numbers object ℕ, i.e. to admit primitive recursion at all S-types, although sobriety of ℕ means that general recursion is also defined (Section A 9–10). The extension of recursion to S-types follows essentially the same argument as in Proposition 4.15 for colimits.
Proposition 6.14
The inclusion S→S preserves ℕ.
Proof The recursion data in the fully parametrised version of this result consist of
| z:Γ→{Y ∣ E} and s:Γ×ℕ×{Y ∣ E} → {Y ∣ E}, |
and we shall prove it symbolically like this in Lemma 8.14. Here, for brevity, we omit the parameters in s.
First, {Y ∣ E} may be expressed as an equaliser as shown.
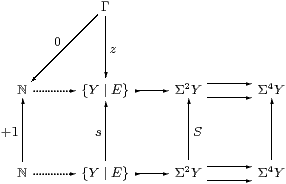
Then use injectivity to extend s:{Y ∣ E}→{Y ∣ E} to endofunctions of Σ2 Y and Σ4 Y, so that s becomes a mediator between equalisers. Then recursion in S defines a map ℕ→Σ2Y that makes the squares commute and also has equal composites to Σ4 Y. Finally, the required map ℕ→{Y ∣ E} mediates to the equaliser. ▫


